Citat:
Ivan Dimkovic: Err.. ne.
Potpuno je nebitno da li mnozis reciprocnom vrednoscu, ili delis - situacije u kojima se susreces sa deljenjem sa nulom su iste, samo ce se desiti ili u procesu generisanja reciprocne vrednosti (1.0/x) ili u procesu deljenja.
Nisi razumeo poentu. Nije stvar u tome da ti imaš vektor kojim treba deliti, ali da prvo izračunaš recipročnu vrednost, pa onda množiš njom, već da u startu radiš sa vektorom kojim treba množiti.
Kada izračunavaš vektor kojim treba deliti, ponegde možeš dobiti nulu, ali da si umesto toga računao vektor kojim treba množiti, dobio bi na tim mestima beskonačnost
ispravnog znaka, tako da ni kasnije sa množenjem ne bi imao problem. Zato je to ispravan dizajn.
Vidiš, svojevremeno sam radio na jednoj grafičkoj aplikaciji, gde je bilo potrebno odrediti najmanji pravougaonik u kome leži neka Bezijeova kriva. Bezijeova kriva je parametarska kriva, kojoj su obe koordinate polinomi po parametru stepena ne većeg od 3, pri čemu se parametar kreće od 0 do 1. Dakle, trebaju mi minimum i maksimum polinoma
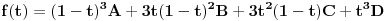
na segmentu [0,1].
Ideja je bila da odredim konačan skup tačaka S takav da se minimum i maksimum na segmentu [0,1] dostižu u nekim od tačaka skupa S, a da onda odredim minimum i maksimum vrednosti u tačkama iz skupa S. Skup S se sastoji od tačaka 0, 1 i onih nula izvoda polinoma koje leže između 0 i 1. Dakle, skup S ima najmanje dve, a najviše četiri tačke. Jasno je da je
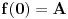
i
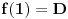
.
Kada se odredi izvod
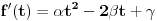
, onda za

(pri čemu se uzima da je
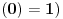
nule izvoda izražavaju numerički stabilnim formulama
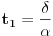
,
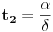
. Naravno, treba voditi računa o delenju nulom i korenovanju negativnih brojeva.
Konačan kod bi mogao da glasi ovako
Code:
#define UPDATE_MIN_MAX(t0)\
float t = t0;\
float t1 = 1 - t;\
float A1 = t1*A + t*B;\
float B1 = t1*B + t*C;\
float C1 = t1*C + t*D;\
float A2 = t1*A1 + t*B1;\
float B2 = t1*B1 + t*C1;\
float f = t1*A2 + t*B2;\
\
if (f < min) {\
min = f;\
} else if (f > max) {\
max = f;\
}
void minmax(float A, float B, float C, float D, float &min, float &max) {
if (A < D) {
min = A;
max = D;
} else {
min = D;
max = A;
}
float alpha = -A + 3*B - 3*C + D;
float beta = -A + 2*B - C;
float gamma = -A + C;
float delta = beta*beta - alpha*gamma;
if (delta >= 0) {
if (beta >= 0) {
delta = beta + sqrt(delta);
} else {
delta = beta - sqrt(delta);
}
if (alpha*delta > 0 && fabs(delta) < fabs(alpha)) {
UPDATE_MIN_MAX(delta/alpha)
}
if (gamma*delta > 0 && fabs(gamma) < fabs(delta)) {
UPDATE_MIN_MAX(gamma/delta)
}
}
}
#undef UPDATE_MIN_MAX
Kod je imun na jednakost najviših koeficijenata sa nulom (kada izvod nije više kvadratna, već linearna jednačina) i sve vrste singulariteta, pod pretpostavkom da ulazne veličine nisu toliko velike da množenjem dolazi do prekoračenja opsega float tipa (tj. da se neće dobiti međurezultat +/-inf), što je u tom grafičkom programu ispunjeno. Da nije, koristila bi se ovakva funkcija, koja poziva prethodnu:
Code:
void huge_minmax(float A, float B, float C, float D, float &min, float &max) {
float mx = 1;
float A1 = fabs(A);
float B1 = fabs(B);
float C1 = fabs(C);
float D1 = fabs(D);
if (A1 > mx) {
mx = A1;
}
if (B1 > mx) {
mx = B1;
}
if (C1 > mx) {
mx = C1;
}
if (D1 > mx) {
mx = D1;
}
float k = 1/mx;
minmax(A*k, B*k, C*k, D*k, min, max);
min *= mx;
max *= mx;
}
Prouči malo ove primere, pa će ti biti jasnije šta je dobar dizajn koda koji nešto računa.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.