Citat:
boxxter: "Uncountable" redirects here. For the linguistic concept, see Uncountable noun.
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the natural numbers.
http://en.wikipedia.org/wiki/Uncountable_set
The best known example of an uncountable set is the set R of all real numbers; Cantor's diagonal argument shows that this set is uncountable. The diagonalization proof technique can also be used to show that several other sets are uncountable, such as the set of all infinite sequences of natural numbers (and even the set of all infinite sequences consisting only of zeros and ones) and the set of all subsets of the set of natural numbers.
http://en.wikipedia.org/wiki/Uncountable_set#Examples
Da, to nije neizračunljivost, već neprebrojivost. Da, tu se koristi dijagonalni argument, mada može i drugačije.
Pretpostavimo da je
niz svih realnih brojeva. Konstruišimo nizove
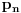
i
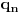
na sledeći način:
,
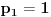
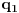
je najmanji prirodan broj veći od
takav da je
.
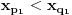
Za
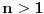
je
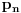
najmanji prirodan broj veći od
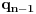
takav da je
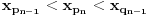
i
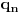
najmanji prirodan broj veći od
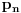
takav da je
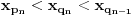
Lako se dokazuje da je definicija korektna, da je
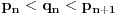
i da za
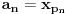
i
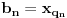
važi
.
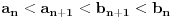
Za
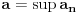
i
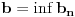
je
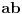
, pa postoji
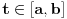
. Neka je
najmanji prirodan broj takav da je
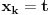
. Jasno je da je
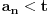
, tj. da
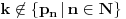
i slično za
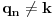
. Razmotrimo prvi član u nizu
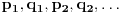
koji je veći od
. Ako je to
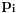
, onda je to u suprotnosti sa njegovim izborom, a ako je to
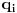
, opet je to u suprotnosti sa njegovim izborom.
Kraj.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Re: Najlepsi dokazi u matematici
