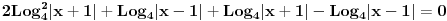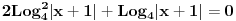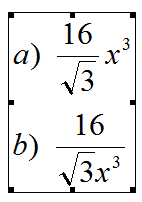[es] - Nekoliko zadataka

LogX

Član broj: 259158
Poruke: 34
*.dynamic.isp.telekom.rs.

+6 Profil

^{21.06.2010. u 11:09 - pre 180 meseci}

1.Zbir prva tri clana rastuceg geometrijskog niza je 91. Ako tim clanovima dodamo redom 25, 27 i 1 dobijamo
tri broja koja obrazuju aritmeticki niz. Sedmi clan datog geometrijskog niza je?

2.Zbir svih resenja jednacine

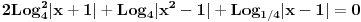
3.Najmanja vrednost rastojanja tacke M(0,-2) od tacaka (x;y) takvih da je

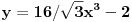za x>0 iznosi?

4.Zbir resenja jednacine

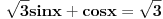koja pripada intervalu (0,

)

Unapred hvala.

Odgovor na temu

bobanex
Boban Mitrovic
Pozarevac

Član broj: 45916
Poruke: 393
*.dynamic.isp.telekom.rs.

ICQ: 54710282
Sajt: matematika-012.tk

+31 Profil

Re: Nekoliko zadataka

^{21.06.2010. u 13:22 - pre 180 meseci}

1.
a+aq+aq^2=91
a+25+aq^2+1=2(aq+27)
resi sistem, uzmi u obzir da je niz rastuci pri odredjivanju q, posle ces lako naci sedmi clan.

4.
(sqrt(3)/2)sinx+(1/2)cosx=sqrt(3)/2
cos(pi/6)sinx+sin(pi/6)cosx=sqrt(3)/2
sin(x+pi/6)=sqrt(3)/2
...

Shoutcast striming za online radio stanice
http://shout-cast.tk
Rešeni zadaci sa prijemnih ispita
http://matematika-012.tk

Odgovor na temu

Cabo
Lokanje u bircuzu

Član broj: 10942
Poruke: 684
*.rcub.bg.ac.rs.

+5 Profil

Re: Nekoliko zadataka

^{21.06.2010. u 15:33 - pre 180 meseci}

Glavni problem kod izraza tipa:

Citat:

LogX:

je što se ljudi demorališu kad vide „šumu“ simbola. Samo polako i pažljivo, korak po korak, i rešićeš. Zadatak uopšte nije težak, samo iziskuje dosta strpljenja i: vremena ili iskustva.

Kliknite da vidite kako da pišete matematičke formule u [tex]TeX[/tex]-u bez slanja slika

Odgovor na temu

LogX

Član broj: 259158
Poruke: 34
*.dynamic.isp.telekom.rs.

+6 Profil

Re: Nekoliko zadataka

^{21.06.2010. u 17:45 - pre 180 meseci}

neverovatno da se nisam setio da postavim takav sistem. Hvala.
Sto se tice logaritama,u sustini glavna stvar je prvo postaviti uslove jel da?

Odgovor na temu

bobanex
Boban Mitrovic
Pozarevac

Član broj: 45916
Poruke: 393
*.dynamic.isp.telekom.rs.

ICQ: 54710282
Sajt: matematika-012.tk

+31 Profil

Re: Nekoliko zadataka

^{21.06.2010. u 21:23 - pre 180 meseci}

Uslove ces postaviti sam a jesu bitni kako ne bi dobio vise resenja nego sto ih realno ima.

Dalje ces lako.

Shoutcast striming za online radio stanice
http://shout-cast.tk
Rešeni zadaci sa prijemnih ispita
http://matematika-012.tk

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2056
212.200.34.*

+391 Profil

Re: Nekoliko zadataka

^{21.06.2010. u 21:35 - pre 180 meseci}

3.Najmanja vrednost rastojanja tacke M(0,-2) od tacaka (x;y) takvih da je...uslov.

d = koren((x-0)^2 + (y+2)^2)

Tražiš funkciji d ektremne vrednosti (minimum).
Formraš Lagranžovu funkciju:
F(x,y,p) = d(x,y) + p*(uslov)
p je parametar.
Dalje znaš?

Ili praktičnije rešenje je da u izraz d = koren((x-0)^2 + (y+2)^2)
direktno zameniš y iz uslova i dobiješ d u funkciji samo od x.
d = koren(x^2 + (256/3)*x^6)
i nađeš joj minimum.
Dalje znaš?

_{[Ovu poruku je menjao miki069 dana 21.06.2010. u 22:50 GMT+1]}

Odgovor na temu

LogX

Član broj: 259158
Poruke: 34
*.dynamic.isp.telekom.rs.

+6 Profil

Re: Nekoliko zadataka

^{21.06.2010. u 21:44 - pre 180 meseci}

Citat:

miki069: 3.Najmanja vrednost rastojanja tacke M(0,-2) od tacaka (x;y) takvih da je...uslov.

d = koren((x-0)^2 + (y+2)^2)

Tražiš funkciji d ektremne vrednosti (minimum).
Formraš Lagranžovu funkciju:
F(x,y,p) = d(x,y) + p*(uslov)
p je parametar.

Dalje znaš?

Ako nesto zapne javicu . Hvala puno. Obicno mi treba samo podstrek kako poceti zadatak a onda mi se javi kako dalje :D

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2056
212.200.34.*

+391 Profil

Re: Nekoliko zadataka

^{21.06.2010. u 22:01 - pre 180 meseci}

Izjednačavanjem izvoda navedene funkcije sa nula dobija se jedino realno rešenje X=0.
Data tačka M(0,-2) pripada grafiku funkcije iz uslova. (jbg tek sad vidim).
Ona je od sebe udaljena nula.
Ali ne ispunjava uslove zadatka jer mora biti x>0.
Tako da je zadatak filozofski.
Koja je to prva tačka do x=0 da ispunjava uslov x>0?

Odgovor na temu

bobanex
Boban Mitrovic
Pozarevac

Član broj: 45916
Poruke: 393
*.dynamic.isp.telekom.rs.

ICQ: 54710282
Sajt: matematika-012.tk

+31 Profil

Re: Nekoliko zadataka

^{21.06.2010. u 22:37 - pre 180 meseci}

Mozda je postavljac teme slucajno napisao pogresno izraz, a ili b?

Shoutcast striming za online radio stanice
http://shout-cast.tk
Rešeni zadaci sa prijemnih ispita
http://matematika-012.tk

Prikačeni fajlovi

Bez naslova.png - 2.9k

Odgovor na temu

LogX

Član broj: 259158
Poruke: 34
*.dynamic.isp.telekom.rs.

+6 Profil

Re: Nekoliko zadataka

^{22.06.2010. u 12:14 - pre 180 meseci}

Citat:

bobanex: Mozda je postavljac teme slucajno napisao pogresno izraz, a ili b?

Pod b :)

Odgovor na temu

miki069

Član broj: 161528
Poruke: 2056
212.200.34.*

+391 Profil

Re: Nekoliko zadataka

^{22.06.2010. u 12:45 - pre 180 meseci}

Kako pod b) kad množenje i deljenje imaju istu prednost?
Onda staviš zagradu i sve bude jasno.

Nema veze, ajd ponovo:
Onda tačka M(0,-2) ne pripada funkciji iz uslova i zadatak ima smisla.
Onda u izraz d = koren((x-0)^2 + (y+2)^2)
direktno zameniš y iz uslova i dobiješ d u funkciji samo od x.
Uradiš joj prvi izvod i isti izjednačiš sa nulom...

Odgovor na temu