Citat:
Dinaaaa: Problem je ovaj deo oko sabiranja integrala.
Ne trebas sabirati te integrale (afaik to bi radila da su ti granice zadanog integrala od 0 do +beskonacno, pa ti treba sabiranje da bi zakljucila o eventualnoj parnosti podintegralne funkcije, te konacni rezultat (ovog sa beskonacnim granicama) samo podijelila sa dva.)
U tvom slucaju (rekla si da je ovo Furierov transform) dovoljno ti je znati *glavnu vrijednost* zadanog integrala. A ta glavna vrijednost zadanog integrala ce postojati ako postoji limes (kad R->besk i r->0) zbroja integrala I1 i I3.
Ti si pokazala da je u slucaju kad R->besk I4=0.
Jos trebas samo izracunati koliki je I2, odnosno njegov limes kad r->0. Ne znam na koji nacin si ga izracunala, ali najjednostavnije je preko tvrdnje:
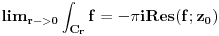
koja vrijedi za analiticke funkcije u okolisu pola z0 (nas pol je 0), gdje sam odmah uracunao da kruzni luk C_r ide u negativnom smjeru od pi do 0.
Nakon sto izracunas reziduum u nuli (jednak je -2i), dobije se da je taj limes jednak
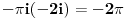
.
Dakle
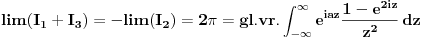
.
Sad jos samo preostaje ovu kompleksnu verziju integrala transformirati u oblik iz kojeg cemo iscitati rjesenje naseg pocetnog integrala. Pri tome uzimamo naravno da je z realno na intervalu integracije, pa trebamo modificirati
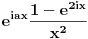
tako da u konacnom izrazu dobijemo
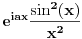
Nakon nekoliko redova trigonometrije (koje sam omaskom pojednostavnio racunajuci da je a=1, a sad mi se ne da ponovo a i bojim se da se da ce se zakomplicirati :) ) dobije se:
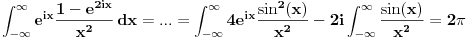
Ovaj zadnji integral je jednak nuli, i dobijemo konacno rjesenje zadanog integrala uz a=1:
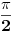
.
Vjerojatno bi trebalo nesto i diskutirati za

u opcem slucaju.
p.s Sve ovo uzmi ipak s rezervom jer sam kompleksnu davno imao a zanimljivo ovaj dio materije uopce nismo obradjivali.
while(sleeping) cat_wails(); wake_up(); for(int i=0;i<9;i++) shoot_cat(); rejoice();
goto(bed);
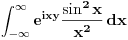
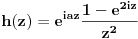 , ali ponovo ne uspevam da dodjem do resenja. Ko zna ili misli da zna nek priskoci u pomoc :)).
, ali ponovo ne uspevam da dodjem do resenja. Ko zna ili misli da zna nek priskoci u pomoc :)).