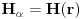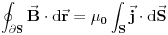i kružnog poprečnog presjeka teče struja I jednoliko raspoređena po njegovom poprečnom presjeku. Odrediti jakost magnetskog polja
i kružnog poprečnog presjeka teče struja I jednoliko raspoređena po njegovom poprečnom presjeku. Odrediti jakost magnetskog polja 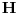 .
.Zadatak imam riješen u knjizi, a riješava se primjenom jedne od Maxwelovih jednačina u diferencijalnom obliku (mada se može riješiti mislim i primjenom integralnog oblika te jednačine). Ta jednačina je poznata i pod imenom Ampèreov kružni zakon i glasi
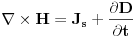 .
.(Alternativni oblik ove jednačine je i
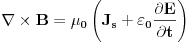 , mada je on nebitan u ovom zadatku, a indeks
, mada je on nebitan u ovom zadatku, a indeks  označava slobodna naelektrisanja).
označava slobodna naelektrisanja).Član
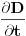 se odbaci, jer nema promjene električnog polja tokom vremena.
se odbaci, jer nema promjene električnog polja tokom vremena.Nadalje, za rješavanje se koristi cilindrični koordinatni sistem, čija se koordinata
 poklapa sa osom vodiča. U matematici je data ova formula za rotor nekog vektora (u ovom slučaju to je
poklapa sa osom vodiča. U matematici je data ova formula za rotor nekog vektora (u ovom slučaju to je 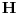 ) u clindričnom koordinatnom sistemu:
) u clindričnom koordinatnom sistemu: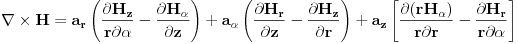
gdje su
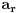 ,
, 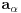 i
i 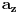 jedinični vektori vezani za koordinate
jedinični vektori vezani za koordinate  ,
,  i
i  cilindričnog koordinatnog sistema respektivno.
cilindričnog koordinatnog sistema respektivno.Nadalje, u knjizi se kaže:
Zbog osne simetrije vrijedi
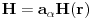 , pa je:
, pa je:i onda je dat izraz za kojeg meni nije jasno kako je dobiven:
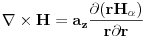
Ako sam dobro zaključivao,
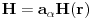 znači da je smjer vektora
znači da je smjer vektora 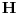 u smjeru vektora
u smjeru vektora 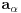 , a da je njegova kvantitativna vrijednost funkcija od
, a da je njegova kvantitativna vrijednost funkcija od  , dakle od udaljenosti od ose. Primjenom rotora, taj vektor pređe u vektor
, dakle od udaljenosti od ose. Primjenom rotora, taj vektor pređe u vektor 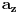 . Ako pogledamo izraz za rotor u cilindričnom koordinatnom sistemu imamo da uz
. Ako pogledamo izraz za rotor u cilindričnom koordinatnom sistemu imamo da uz 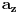 stoji
stoji 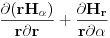 od čega samo uzmemo
od čega samo uzmemo 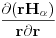 , jer se jedino u tom članu
, jer se jedino u tom članu  mijenja.
mijenja.[Ovu poruku je menjao R A V E N dana 04.05.2010. u 18:15 GMT+1]




 Kako dobiti ovo (da li sam pravilno razmišljao)? - klasični elektromagnetizam
Kako dobiti ovo (da li sam pravilno razmišljao)? - klasični elektromagnetizam