Citat:
Nemanjich: Mozes li mi reci neki konkretan razlog zasto je Ivanoviceva Kvantna losa? Ne bih bas da bacam 1150 strana bez razloga. Meni deluje nekako enciklopedijskog karaktera, u smislu da ima i istorijskih stvari, sto je dobro za opstu kulturu inzenjera Fizicke elektronike ili Diplomiranog Fizicara. A pored toga cini mi se da ima dosta stvari obradjeno. Sa druge strane nisam je nesto previse konzumirao, da bih dao neku ocenu strucnosti.
A za operatore:
Koji je motiv za koriscenje operatora? Zbog cega ih nismo koristili u fizici 1,2 (Njutnova mehanika, fluidi, termodinamika...)? Pretpostavljam da moze, na neki slican nacin kao u KM. Nekako mi sva ta prica sa operatorima deluje aksiomatskog karaktera, i iskreno nisam se bas navikao na nju. Shvatam formalizam koji se tu koristi bez problema, ali mi fali neka fizicka interpretacija svega toga, ili neka intuicija pri radu sa njima.
Dok ovo pisem pade mi na pamet da se njima lakse zapisuju komplikovane jednacine, npr SJ.
Tek sad videh ovo.
Ima puno gresaka. Covek je uspeo da na 1150 strana dotakne neverovatno malo stvari, sto da je hteo verovatno ne bi uspeo.
Probacu da ti objasnim na primeru. U klasicnoj mehanici ti imas funkcije koje istovremeno zavise i od polozaja i od impulsa
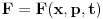
i posmatrajuci jednacine kretanja (ovih dinamickih varijabli) ti definises strukture koje se nazivaju Poasonove zagrade, koje se u literaturi najcesce oznacavaju
.
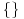
U kvantnoj mehanici ti ne mozes znati istovremeno i polozaj i impuls cestice pa uvodis tzv. teoriju reprezentacija. Pa imas neko
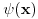
u koordinatnoj reprezentaciji, i neko
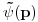
u impulsnoj reprezentaciji npr., a vezu izmedju ovih talasnih funkcija ti daje Furije transformacija. Isti ti je vrag naravno sta ces reci da je Furije-original, a sta Furije - lik.
Da bi imao kvatnu mehanicku interpretaciju i
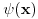
i
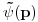
trebaju da budu
funkcije. Ako je jedna od njih
fja i druga je. Ovo ti obezbedjuje Parsevalov identitet!
U linearnoj algebri postoji nesto sto se zove karekteristicna jednacina, u KM se zbog englesko-nemackog uticaja obicno koristi naziv svojstveni problem (eigen problem). U kvantnoj mehanici opservable (dinamicke varijable) preuzimaju ermitski operatori jer oni imaju realne svojstvene vrednosti, a ulogu Posanovih zagrada komutatori
. I imamo lepu fizicko - matematicku vezu. Operatore, koji predstavljaju fizicke velicine koje se mogu simultano meriti, mozes simultano da dijagonalizujes, odnosno njihov komutator je nula, i ta dva operatora imaju
zajednicku svojstvenu bazu. Ovo poslednje je bitno jer dva operatora mogu imati neke zajednicke svojstvene vektore, a da ne komutiraju.
To je neka prica, odnosno grebanje po povrsini ove price!
Re: Kvantna Mehanika
Registrovani: 3 ( vjova, Bojan Basic, Nebojsa Milanovic )
