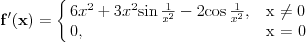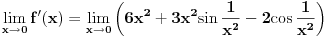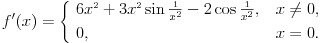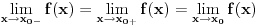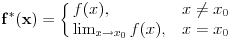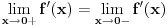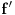Da funkcija nije dodefinisana, uopste ne bismo mogli traziti izvod u nuli jer ne bi pripadala domenu funkcije.
Nekako mi je tesko prihvatiti da je izvod definisan sa
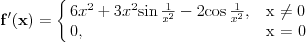
samo iz razloga sto je izvod takodjer funkcija. Da bi dodefinisali funkciju u nekoj tacki
, zar ne mora da bude:
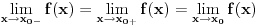
te se tada funkcija dodefinise kao:
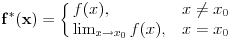
U ovom slucaju taj limes ne mozemo naci, tako da ne razumijem kako mozemo pisati da je vrijednost funkcije (tj. izvoda) u nuli -- nula.
Citat:
Funkcija je neprekidna (na celom svom domenu), diferencijabilna je u nuli, i izvod postoji u tački nula, kao i van nje, ali nije neprekidan.
Da li ovo znaci da izvod ima prekid u nuli ili 'van nje'... Ne vidim kako bi se prekid mogao naci negdje drugo, a ako je u nuli, onda funkcija nema izvoda u nuli... :S
Cini mi se da se samo vrtim u krug, ovdje, te da mi fali neki teoretski dio, ali sve sto sam nasao da ima veze sa prekidima izvoda je bila
teorema o tackama prekida izvoda (i njene posljedice) ali se ona ne odnosi na ovu situaciju... Ako bi me neko mogao uputiti u pravom smjeru bio bih zahvalan.
[Edit]
Citat:
Vrste prekidnosti neke f-je (ovde mislim na ovaj famozni izvod funkcije) su:
- OTKLONJIV PREKID: ako su levi i desni limes konačni i jednaki. Onda se može dodefinisati i biti diferencijabilna.
- NOTKLONJIV PREKID: ako su levi i desni limesi konačni i nisu jednaki.
- VERTIKALNA ASIMPTOTA: ako je bar jedan limes beskonačan
Mislim da je Čabo u pravu 100%.
Iako ih ne znamo (oba limesa "divljaju") znamo da su između sebe jednaki.
OTKLONJIV PREKID.
Dosta dobar primer.
Tosgin: je li ovo sa matematičkog fakulteta ili nekog tehničkog?
Postao si dok sam ja pisao... ;)
Eh, pa upravo to je stvar... mozemo zakljuciti da je prekid otklonjiv, ali ne znamo koja mu je vrijednost, te samim tim ne mozemo znati ni vrijednost izvoda u tacki nula? :D
I, ne, nije matematicki fakultet, vec elektrotehnicki.
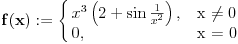
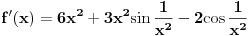
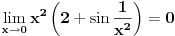
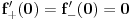
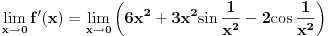
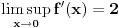
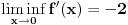
Izvod funkcije koja je dodefinisana za neku tacku
