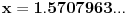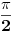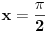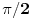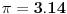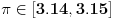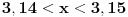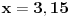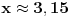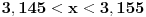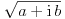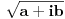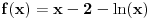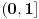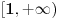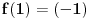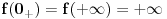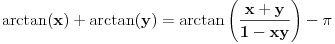Citat:
holononi: To smo i hteli da čujemo. Da nismo toliko odugovlačili sa pričom kako Mathematica računa, onda bi rešenje možda bilo prihvatljivo, tu je izmedju 3.14-3.15. A šta bi sa drugim rešenjem?
Već sam odgovorio na to. Da je bilo bilo šta bitno, naravno da bih našao oba i to samo pomoću olovke i papira. Pročešljaj malo ovaj forum, pa vidi šta sam sve rešavao, naročito 2005, kada sam bio najaktivniji - kudikamo složenije stvari od ove pišljive jednačine.
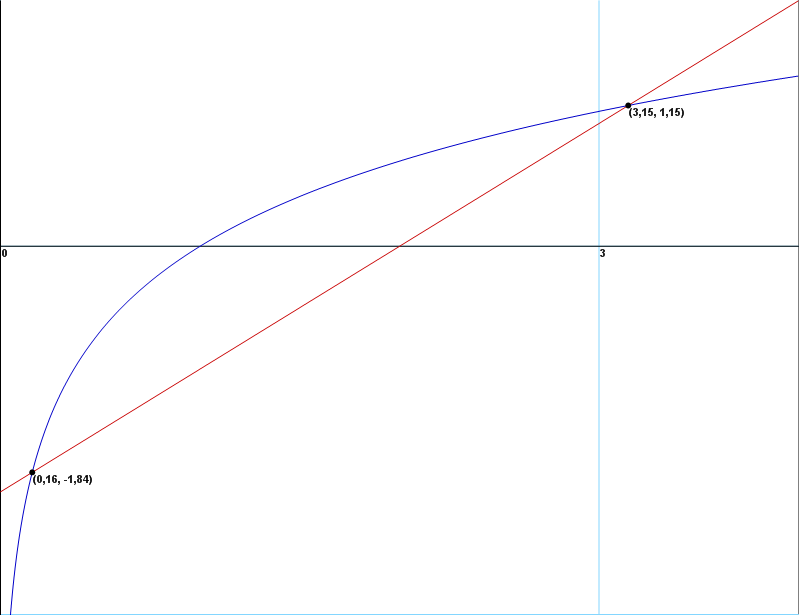
Konkretno, funkcija
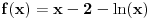
je jasno da pada natervalu
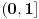
, a raste na intervalu
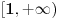
, kao i da je neprekidna i da je
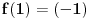
i
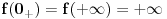
. Računanje izvoda pri rešavanju jednačina i dokazivanju nejednačina je tipična stvar.
Inače, postoji algoritam koji za ma koju glatku funkciju lokalizuje sve njene korene na kompaktu, ako nema višestrukih i ako ih je konačno mnogo, kao i mehanička procedura koja bi rešila zadatke ove, pa i kudikamo veće složenosti.
Citat:
holononi: U tom smislu, lično bih prihvatio oba rešenja kao polaznu tačku, pa bih i oba proverio. U tome je prednost primene računara. Ne u nekom konačnom i nepogrešivom.
Evo, zanima me koliko je ln(1.7) na 5 decimala. Windows-ov kalkulator kaže da je 0.53063. Kako to da proverim? Da računam na ruke? A šta će mi onda računar? Da bih uporedio rezultate?
Koliko ja shvatam, smisao wolframovog paketa je "da korisnik bude zadovoljan", a obzirom da raja tipično ne zna matematiku ni onoliko koliko je koristi, to znači da za svaki ulaz softver treba da napiše nešto na ekranu - imalo to smisla ili ne.
BTW, ako vam grafici toliko znače, program wxMaxima je besplatan i može to i još mnogo toga. Ne morate davati Wolframu na hiljade evra za to. Program Graph je kvalitetan softver za crtanje 2D grafika (jeste da bi se mogao mnogo ubrzati upotrebom jednostavnog, a mnogo bržeg algoritma, ali važno je da ne brljavi), nije besplatan, ali je kudikamo jeftiniji od Wolframa.
Citat:
holononi: Upravo u tome je i bila poenta postavljenog zadatka. Jednačina ima dva rešenje. Medjutim da li postoji jedinstven postupak da se dobiju oba rešenja? Ako ne, kako dobiti jedno a kako drugo rešenje?
Mathematica daje oba rešenja.
Takav postupak itekako postoji.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 je simbolička promenljiva u ovom prvom slučaju. Matematika je inače vrlo precizna kada je reč o nedorečenim uslovima. Na primer,
je simbolička promenljiva u ovom prvom slučaju. Matematika je inače vrlo precizna kada je reč o nedorečenim uslovima. Na primer,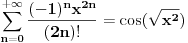 u kompleksnom području. Vrlo precizno, nema šta.
u kompleksnom području. Vrlo precizno, nema šta.



 Re: pomoc oko sinus - cosinus
Re: pomoc oko sinus - cosinus