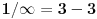Re: Dužina kružnice „iznutra“ i „spolja“Apsen, "Repetitorij više matematike", II dio, Tehnička knjiga, Zagreb, 1964., str. 34.
Tu je dato da je zakrivljenost kružnice polumjera r data kao 1/r i naglašeno je da je zakrivljenost konstanta. U novijoj literaturi se koristi termin krivina krive i definiše se nešto strože pomoću limesa ili izvoda. Ali se suštinski svodi na 1/r. Pogledati na primer
Adnadjević, Kadelburg, "Matematička analiza II" treće izdanje, Nauka, Beograd, 1999., str 100.
ili
Lazarević, "Višedimenzionalna matematička analiza 1", Orion art, Beograd 2003., str. 314.
ili dato nešto jednostavnije u
Mihailović, Janić, "Elementi matematičke analize I", Naučna knjiga, Beograd, 1990., str. 308.
Problem dužine krive se rešava aproksimacijom pomoću upisanih i opisanih mnogouglova, što je već napomenulo više diskutanata na ovom forumu. Razlika je samo u tome što se u prvom slučaju govori o supremumu a u drugom slučaju o infimumu. Kako je LIMES jedini ispravan aparat u matematici za rukovanje beskonačno malim i beskonačno velikim veličinama to se isti primenjuje i u ovakvim slučajevima. Limes i njegovi sledbenici, izvod i integral su omogućili izvodjenje stavova o objektima koji se ne mogu predstaviti "opipljivim" sredstvima. Da su tako izvedeni zaključci ispravni pokazuje se u praksi svakodnevno,
Na primer, pri odredjivanju broja binarnih sudara molekula gasa, odgovarajućim transformacijama na polarne koordinate, dobije se da je
. Ovde je element zapremine predstavljen proizvodom dve beskonačno male veličine, gde su dx i dy priraštaji vektora brzine c. Za detalje pogledati
Yeremin, "The Foundations of Chemical Kinetics", Mir publishers, Moscow, 1979., str. 158.
Rešenje pomenutog problema ima svoj ekvivalent poznat svakom srednješkolcu kao uticaj temperature na brzinu hemijske reakcije. Pogledati na primer
Rakočević, Horvat, "Opšta hemija za I razred srednje škole", Zavod za izdavanje udžbenika i nastavna sredstva, Beograd, 2006., str. 86.
Takodje, u istom udžbeniku su navedeni praktični ogledi kojima učenik može da proveri ponešto od opisanih pojava. Ovim je pokazan primer "svodjenja apstraktnog na konkretno". Neopipljivi pojmovi beskonačno malih veličina su našli svoju potvrdu u materijalnim eksperimenima, dostupnim svima na proveru. Ovo je takodje i osvrt na primedbu "ne može ni da kaže ništa drugo osim onog što je naučio i to bez razumevanja". Jer, pod razumevanjem se smatra da učenik ume da povezuje različite oblasti iste discipline a ovde je učinjeno više pa su povezane oblasti iz različitih disciplina.
Prema tome, svaka nova teorija, koja treba da pobije nešto od postojećih, moraće da dobro pripazi da ne dodje u koliziju sa raznim pojavnim oblicima danas važećih terija (koje nisu proizvod pukog maštanja, već rezultat rada velikog broja istraživača ne samo kroz prostor već i tokom vremena). Sve te teorije se dopunjuju i doradjuju u skladu sa novospoznatim istinama. U tom smislu "rušenje" postojećih definicija u matematici predstavlja "borbu sa vetrenjačama".
