[es] - Dužina kružnice „iznutra“ i „spolja“

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
195.222.97.*

+2801 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 13:09 - pre 194 meseci}

Što se tiče metra, strogo gledano on nije matematički pojam, jer se njegova definicija oslanja na svetlost i atom cezijuma. Međutim, to ne predstavlja problem u davanju odgovora na Galetovo pitanje

Citat:

galet@world: Nedeljko imam za tebe par pitanja:
1. Koliko zajedničkih tačaka ima kružnica prečnika od 2 metra sa svojom tangentom?
2. Koliko zajedničkih tačaka ima kružnica prečnika od 3 metra sa svojom tangentom?

Dakle, kada se izabere jedinična duž, onda se ova pitanja mogu postaviti sa kružnicama prečnika 2 i 3. Stoga ovde nema svrhe cepidlačiti sa metrom, jer je pitanje sasvim jasno. Deder da dam i odgovor.

Svaka kružnica ima sa bilo kojom svojom tangentom tačno jednu zajedničku tačku.

Elem, da se vrnem na razlog zašto sam Galetu postavio ova pitanje.

Ako se ne varam, Galet se slaže s tim da postoji tačno jedan realan broj a takav da za bilo koji broj b važi a+b=b+a=b. E, pa vidiš, to je definicija nule. Nula je po definiciji realan broj u oznaci 0 takav da za ma koji realan broj x važi 0+x=x+0=x. Zamenjujući x sa 0, dobijamo da je 0+0=0.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

mokelet
Beograd, Vozdovac

Član broj: 89322
Poruke: 299
*.dynamic.sbb.rs.

+20 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 13:16 - pre 194 meseci}

Citat:

holononi: Kako nema posebnih uslova podrazumeva se da je "metar" dat definicijom internacinalnog sistema mernih jedinica.

S obzirom da je u tom slučaju "metar" zadat sa tačnošću od

(http://sr.wikipedia.org/sr-el/Metar), mislim da ne možemo da utvrdimo da li tangente zaista dodiruju kružnice prečnika 2 i 3 metra, naročito uzevši u obzir http://sr.wikipedia.org/sr-el/Relacije_neodre%C4%91enosti.

"Ima jedna vračarija za taj strav od vampiri. Kad se nekoj mlogo plaši, ja mu malko prebajem. Uznem jedno perce od crnu kokošku, jednu rženu slamku i malko bosiljak. Toj držim u ruku, a taj čovek što ga strav, on se krsti a ja bajem: "Otud ide crna kvačka, vodi crni piliki, dovede gi na crno bunjište, tuj čeprljaše i raščeprljaše, s kljunice iskljucaše, i raznesoše i odletoše."

holononi

Član broj: 163572
Poruke: 658
91.148.88.*

+5 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 13:29 - pre 194 meseci}

Relcija neodredjenosti nije potrebna u ovom slučaju jer @galet@world verovtno napada prethodno date definicije. A osim toga relacija neodredjenoti se pre uklapa u "neodredjenost" realnog broja.

galet@world

Član broj: 81985
Poruke: 1076
*.adsl-a-2.sezampro.yu.

+3 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 15:28 - pre 194 meseci}

Citat:

Nedeljko:
Svaka kružnica ima sa bilo kojom svojom tangentom tačno jednu zajedničku tačku.

Prava je određena sa dve tačke ili sa jednom i smerom, a smer određuju susedne tačke kod
svake krive. Dosad je tangenta uvek prolazila kroz dve tačke. Bar smo tako učili, ali dobro,
pretpostavljam šta misliš - tangenta prolazi kroz jednu tačku a smer joj je normalan na radijus
zakrivljenosti u toj tački. Ovo je prihvatljivije od onog što sam učio o tangenti. OK.
Prava koja prolazi kroz dve susedne tačke odnosno deo prave koji prolazi kroz te tačke je
usvari granična tetiva.
Imaš li primedbu ili možda neko treće objašnjenje?

japan

Član broj: 34328
Poruke: 480
87.250.50.*

+13 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 15:49 - pre 194 meseci}

Citat:

galet@world: Prava koja prolazi kroz dve susedne tačke odnosno deo prave koji prolazi kroz te tačke je
usvari granična tetiva.

šta su to susedne tačke?

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
195.222.97.*

+2801 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 16:35 - pre 194 meseci}

Galet, ključna je ova stvar, koju ne komentarišeš:

Citat:

Nedeljko: Ako se ne varam, Galet se slaže s tim da postoji tačno jedan realan broj a takav da za bilo koji broj b važi a+b=b+a=b. E, pa vidiš, to je definicija nule. Nula je po definiciji realan broj u oznaci 0 takav da za ma koji realan broj x važi 0+x=x+0=x. Zamenjujući x sa 0, dobijamo da je 0+0=0.

Molim te da obavezno odgovoriš na ovo.

A što se prave tiče, svaka prava prolazi kroz beskonačno mnogo tačaka, a jednoznačno je određena sa bilo koje dve ili sa jednom i sa pravcem. Opšta definicija tangente ide preko izvoda, ali ono što definitivno ne mogu da prihvatim su susedne tačke.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

galet@world

Član broj: 81985
Poruke: 1076
*.adsl-a-2.sezampro.yu.

+3 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 17:47 - pre 194 meseci}

Citat:

Nedeljko: Galet, ključna je ova stvar, koju ne komentarišeš

Ne brini, komentarisaću.
Pretpostavljam da nemaš primedbi na moje razmišljanje o tangenti jer tu nisi stavio primedbu.
Primedba se, prema tome, odnosi na tetivu.
Tetiva je duž koja spaja dve tačke na kružnici. Dužina tetive je rastojanje između tih tačaka.
Kolika je dužina granične tetive?
(Valjda znaš šta je granična ili najmanja tetiva ili ćeš opet da tražiš definiciju??)

mokelet
Beograd, Vozdovac

Član broj: 89322
Poruke: 299
*.dynamic.sbb.rs.

+20 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 18:22 - pre 194 meseci}

Citat:

galet@world:
(Valjda znaš šta je granična ili najmanja tetiva ili ćeš opet da tražiš definiciju??)

Za sve vreme studiranja matematike nisam čuo za graničnu ili najmanju tetivu.
A koliko vidim, nije čuo ni Google: ""granicna tetiva"" i Google: ""najmanja tetiva""

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
195.222.97.*

+2801 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 18:32 - pre 194 meseci}

Citat:

galet@world: Pretpostavljam da nemaš primedbi na moje razmišljanje o tangenti jer tu nisi stavio primedbu. Primedba se, prema tome, odnosi na tetivu. Tetiva je duž koja spaja dve tačke na kružnici. Dužina tetive je rastojanje između tih tačaka.
Kolika je dužina granične tetive?(Valjda znaš šta je granična ili najmanja tetiva ili ćeš opet da tražiš definiciju??)

Kako nemam? Oslanjaš se na nepostojeći pojam "susednih tačaka". Gde god da su tačke A i B, postoji središte duži AB koje je između njih. Naravno da ne znam šta je granična tetiva, niti najmanja tetiva.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

holononi

Član broj: 163572
Poruke: 658
91.148.95.*

+5 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 18:35 - pre 194 meseci}

U postu od 01.05.2009. u 13:06h navedeno je da se ne mogu izolovati dve susedne tačke u skupu realnih brojeva. Moguće je izolovati jednu tačku, ali kad se izoluje ta tačka tada nije moguće preći na sledeću susednu. Jer u skupu realnih brojeva izmedju svaka dva realna broja postoji realan broj. I taj proces se nikad ne završava.

Pojam granične tetive niuje definisan.

Kad su u pitanju kružnica i tangenta onda može da se postavi bolje pitanje. Naime, za očekivati je diskusije na temu šta je sa tangentom prave koja je u stvari kružnica beskonačnog prečnika. Koliko takva kružnica i njena tangenta imaju zajedničkih tačaka i to sve po definiciji izvoda.

japan

Član broj: 34328
Poruke: 480
87.250.50.*

+13 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 19:19 - pre 194 meseci}

Citat:

galet@world: Valjda znaš šta je granična ili najmanja tetiva ili ćeš opet da tražiš definiciju??

ja ne znam šta je to granična tetiva. pretpostavljam da je to duž koja spaja "susedne tačke" na kružnici?

galet@world

Član broj: 81985
Poruke: 1076
*.adsl-a-2.sezampro.yu.

+3 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 20:11 - pre 194 meseci}

Ako susedne tačke nisu definisane to ne znači i da ne mogu biti, a pogotuvu da ne postoje.
Postojanje nečega ne zavisi valjda od postojanja definicije. Činjenica je da tetive postoje
i da je najveća jednaka prečniku kružnice, činjenica je takođe da postoji tangenta koja nije
tetiva.
Maksimalna dužina tetive je prečnik, a koja je minimalna ponovo pitam.
Izjava "Naravno da ne znam šta je granična tetiva, niti najmanja tetiva" je poražavajuća.
To uopšte nije "naravno", osim ako ne uvedemo princip da za sve što ne znamo kažemo da je naravno
Kako se može u matematici ostaviti pojam tetive u tolikoj meri nedorečen?
Pokušajte bar preko limesa.

holononi

Član broj: 163572
Poruke: 658
*.adsl.beotel.net.

+5 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 20:21 - pre 194 meseci}

Citat:

šta je to granična tetiva. pretpostavljam da je to duž koja spaja "susedne tačke" na kružnici?

Ako je to definicija granične tetive opet ostaje problem izolovanja susednih tačaka. Kad bi mogli da izolujemo dve susedne tačke u skupu realnih brojeva, tada bi mogli da sve realne brojeve poredjamo u niz. Posle svakog realnog broja dolazio bi sledeći realan broj. Dobili bi da je skup realnih brojeva poredjan u niz pa tim i prebrojiv. Medjutim, skup realnih brojeva nije prebrojiv. Za dokaz, pogledati tvrdjenje Kantora o neprebrojivosti intervala. Takodje pogledati aksiom neprekidnosti i njegove posledice.

galet@world

Član broj: 81985
Poruke: 1076
*.adsl-a-2.sezampro.yu.

+3 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 22:33 - pre 194 meseci}

Pogledajmo malo ovaj rezon:
Ako imamo neki četvorougao A B C D pa mu smanjujemo recimo stranu C D
Četvorougao ostaje kao pojava sa svojim svojstvima sve dok postoje uglovi C i D
odnosno stranica C D. Onog trenutka ( ne bi trebalo uzimati vremenske termine ali...)
kad tačka C i D budu na istom mestu dobijamo trougao - dakle novu pojavu - taj
prelaz događa se odjednom skokovito a ne postepeno.
Isto tako ako neka prava preseca kružnicu u dve tačke A i B - deo te prave je tetiva.
Ako tu pravu rotiramo oko tačke B tako da se dužina tetive smanjuje t. j. da se tačka
A približava tački B tetiva će se kontinualno smanjivati. Dok god postoji tačka A na
nekom mestu na kom nije tačka B - tetiva postoji. U trenutku kada tačka A padne
na mesto tačke B tetiva više ne postoji - prava je prešla u novu pojavu postala je
tangeta i to skokovito - odjednom. Ako je tačka A krećući se kontinualno došla na
isto mesto gde se nalazi tačka B onda je neposredno pre toga morala biti i susedna
tačka tački A. U tom trenutku tetiva još uvek postoji jer postoje dve tačke, a
rastojanje između njih je nula i ta nula ima dimenziju dužine upravo zato što tu još nije
jedna tačka nego dve.

japan

Član broj: 34328
Poruke: 480
87.250.50.*

+13 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 22:50 - pre 194 meseci}

tačke realnoj pravoj, kružnici, ili čemu god, nisu klikeri pa da mogu biti susedni u jednom trenutku, ili da se poklapaju u nekom drugom. lepo si dobio objašnjenje da između dve različite realne tačke uvek postoji beskonačno mnogo tačaka.

a reci mi galet, znaš li ti koja je razlika između realnih i racionalnih brojeva?

holononi

Član broj: 163572
Poruke: 658
*.adsl.beotel.net.

+5 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{03.05.2009. u 23:21 - pre 194 meseci}

Citat:

postoje dve tačke, a rastojanje između njih je nula

Rastojanje izmedju dve tačke, recimo x i y, d(x,y) = 0 ako i samo ako x = y.

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{04.05.2009. u 07:42 - pre 194 meseci}

Citat:

galet@world: Ako je tačka A krećući se kontinualno došla na isto mesto gde se nalazi tačka B onda je neposredno pre toga morala biti i susedna tačka tački A.

Pojam "neposredno pre" (tj. susednih trenutaka) je sporan kao i pojam susednih tačaka. Tu nema suštinske razlike.

Citat:

galet@world: Ako susedne tačke nisu definisane to ne znači i da ne mogu biti, a pogotuvu da ne postoje. Postojanje nečega ne zavisi valjda od postojanja definicije.

Iz pretpostavke da postoje se dobija kontradikcija (jer svaka duž ima središte), što svakako znači da ne postoje.

Citat:

galet@world: Kako se može u matematici ostaviti pojam tetive u tolikoj meri nedorečen?

Tetiva je sasvim dorečen pojam - duž koja spaja dve tačke kruga. Ako sadrži te dve tačke, onda je zatvorena, ako ih ne sadrži, onda je otvorena.

Citat:

galet@world: Pokušajte bar preko limesa.

U limesu tetiva prelazi u tačku.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

galet@world

Član broj: 81985
Poruke: 1076
*.adsl-a-2.sezampro.yu.

+3 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{04.05.2009. u 09:19 - pre 194 meseci}

Citat:

holononi: Rastojanje izmedju dve tačke, recimo x i y, d(x,y) = 0 ako i samo ako x = y.

To je ipak samo kazivanje, ali ne i dokazivanje. Osim toga u ovom slučaju nema rastojanja jer se ne radi o dve tačke, odnosno
o dva mesta nego o jednom istom mestu pa govoriti o rastojanju nekog mesta od samog sebe nema smisla jer ono ne postoji.

Ako ima smisla govoriti o tome onda ta nula označava nepostojanje i to je nula koja se dobija oduzimanjem dveju
jednakih veličina na pr.: a - a = 0. Takva nula nema dimenziju ma šta označavali simboli a t.j. imali oni dimenziju
ili ne.

Nedeljko, na primer, kaže da je

Ova jednakost nije istinita. Ako, na primer, cifre 1 i 3 označavaju neke dužine onda desna strana ove jednačine predstavlja
nulu bez dimenzije - ta strana označava nepostojanje dužine odnosno nepostojanje uopšte. Leva strana označava nulu koja
ima dimenziju dužine jer je dužina 1 podeljena na beskonačno mnogo delova i ona se opet može dobiti obrnutim postupkom.

Ranije sam naveo primer da samo tačke na preseku dveju ravni pripadaju obema ravnima. Ako isključimo te tačke onda dve
ravni više ne postoje nego četiri poluravni sa međusobnim rastojanjem nula.

Dakle postoje dve različite nule
1. Nula koja označava nepostojanje i koja nema dimenziju - to je nula koja je definisana i koju sad komentarišem
2. Nula koja ima dimenziju i koja je uporediva sa drugim takvim nulama o čemu navodim primer u prilogu

Za nulu pod 1. važi da je n•0 = 0 jer od nepostojanja se ne može dobiti ništa čak i ako je

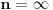
jer
ta nula nema dimenziju ni dužine ni površine niti bilo čega pa ni rezultat ne može imati dimenziju
Za nulu pod 2. to ne važi jer je proizvod n•0 veći od takve nule n puta i tu je pogrešno pisati n•0 = 0, a ukoliko
je

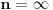
onda je rezultat konačna veličina sa dimenzijom koju ima ta nula. Ovde bi, naravno, trebalo
dodefinisati još mnogo toga, ali ovo za sad predstavlja samo ideju neukog čoveka koju neki vrsan i učen matematičar
može razraditi, proveriti i definisati.

Izvini Nedeljko tvoju poruku sam video tek pošto sam poslao moju pa ću zasad da ti odgovorim samo na ovo

Citat:

U limesu tetiva prelazi u tačku.

Limes neke pojave ne može biti neka druga pojava

_{[Ovu poruku je menjao galet@world dana 04.05.2009. u 10:34 GMT+1]}

Prikačeni fajlovi

Različite nule.doc - 28.5k

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: Dužina kružnice „iznutra“ i „spolja“

^{04.05.2009. u 10:52 - pre 194 meseci}

Citat:

galet@world: To je ipak samo kazivanje, ali ne i dokazivanje. Osim toga u ovom slučaju nema rastojanja jer se ne radi o dve tačke, odnosno o dva mesta nego o jednom istom mestu pa govoriti o rastojanju nekog mesta od samog sebe nema smisla jer ono ne postoji.

To je sastavni deo definicije metrike, a definicije se ne dokazuju. To je kao kada bi dokazivao oznake.

Ako se govori o konkretnoj metrici, recimo rastojanju tačaka u ravni, onda se za uvedenu funkciju mora prvo dokazati da zadovoljava aksiome metrike, da bi se onda ona koristila kao funkcija rastojanja.

Za tačke

euklidsko rastojanje između njih se definiše kao

. Do sada je koren iz svakog pozitivnog realnog broja bio pozitivan realan broj, pa ako je koren nekog realno broja 0, onda je taj realan broj 0. Zbir kvadrata dva realna broja od kojih je bar jedan različit od 0 je pozitivan, pa ako je zbir dva kvadrata realnih brojeva 0, onda su ti realni brojevi jednaki 0. Ako je razlika dva realna broja 0, onda su ti realni brojevi jednaki. Tačke sa istim koordinatama su jedna ista tačka.

Citat:

galet@world: Limes neke pojave ne može biti neka druga pojava

Za ovo ćeš morati da definišeš pojam pojave i pojam limesa pojave.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.