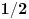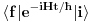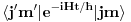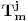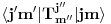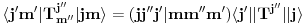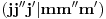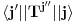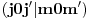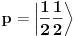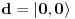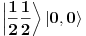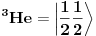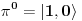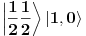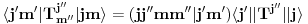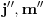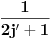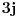Citat:
petarm: Ono sto znam sigurno je da je spin protona
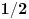
. :)
Ne figuriše ovde spin, već izospin,a ono sa čime si se sreo ovde je zapravo primena Vigner-Ekartovog teorema.
Ovaj proces se dešava čisto preko jake interakcije, koja ima SU(2) simetriju u izospinskom prostoru. Verovatnoća prelaza iz početnog u krajnje stanje je data S-matričnim elementom
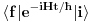
Ovde razmatramo samo hamiltonijan jake interakcije, pošto je samo on relevantan za ovaj proces. Pošto hamiltonijan deluje samo u izospinskom prostoru iz skalarnog proizvoda možemo da faktorišemo skalarni proizvod u orbitnom, spinskom i drugim unutrašnjim prostorima u konstantu, tako da je jedina relevantna stvar u principu sledeći skalarni proizvod u izospinskom prostoru
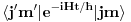
gde su j,m,j',m' izospinski kvantni brojevi početnog i krajnjeg stanja (izospinski j i m su potpuno analogni spinskim j i m - te stoga i naziv "izospin"). Hamiltonijan, te stoga i funkciju hamiltonijana, možemo razviti po ireducibilnim tenzorima SU(2) grupe, tj. po operatorima koji se pri dejstvu SU(2) grupe transformišu kao vektori. Ireducibilni tenzori se stoga karakterišu istim kvantnim brojevima, kao i vektori, tako da ireducibilne tenzore obeležavamo sa
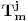
. Kada evolucioni operator razvijemo po ireducibilnim tenzorima, imaćemo skalarne proizvode forme
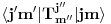
Ovde uskače Vigner-Ekartov teorem koji kaže da je
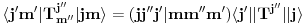
gde je
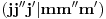
Klebš-Gordanov keficijent, a
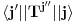
tzv. redukovani matrični element koji nama ovde u principu nije bitan tako da neću pisati izraz za njega, ali je bitno samo uočiti da on uopšte ne zavisi od m, m' i m''.
Pošto je ovde konkretno reč o Hamiltonijanu jake interakcije, a jaka interakcija ima približnu izospinsku SU(2) simetriju sledi da je hamiltonijan skalar grupe, što znači da se on ponaša po 0 reprezentaciji, tj (j=0) (ako se setiš spina, znaš da za s=0 imamo 1D, tj. skalarnu, reprezentaciju) tako da imamo da su Klebš-Gordanovi koeficijenti zapravo
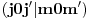
, a redukovani matrični elementi nisu bitni, jer mi zapravo tražimo odnos verovatnoća dešavanja dva procesa za koje imamo isti redukovani matični element tako da će se oni pokratiti pa ne utiču na rezultat. Dakle rezultat je jednak odnosu Klebš-Gordanovih koeficijenata.
Sada ih samo treba naći. Za reakciju
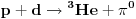
na početku imamo
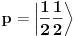
i
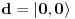
tako da je početno stanje
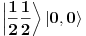
. Na kraju imamo
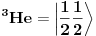
i
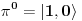
, tj. ukupno stanje
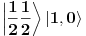
. Odgovarajući Klebš-Gordanov keficijent je 1/3.
Analognim postupkom se za drugu reakciju dobija 2/3 tako da na kraju imamo da je reakcija
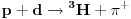
dva puta verovatnija od
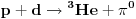
.
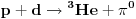
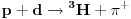
 je proton,
je proton,  deuteron (jezgro deuterijuma), a
deuteron (jezgro deuterijuma), a  pion? Jel tacno?
pion? Jel tacno? 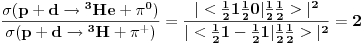




 Nuklearna fizika
Nuklearna fizika