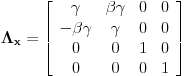Srodne teme

16.01.2003. teorija algoritama?
11.01.2010. Gravitacija - Kvantna teorija ...
08.05.2003. identifikacija broja (sa kompjuterom)
19.05.2003. verovatnoća i statistika-literatura
11.02.2004. Maturski rad - teorija relativnosti
16.01.2009. Knjiga za teoriju relativnosti
03.10.2005. Teorija relativnosti - pod lupom, (alternativno t..
04.04.2005. dopplerov efekt i hubbleov zakon
30.12.2005. teorija skupova-kardinalni brojevi
03.01.2006. rotacijski luk - teorija

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.

Teorija Relativnosti

elitemadzone.org :: MadZone :: Teorija Relativnosti
(Zaključana tema (lock), by Tyler Durden)
Strane: << < .. 86 87 88 89 90 91 92 93 94 95 ... Dalje > >>

[ Pregleda: 468991 | Odgovora: 2583 ] > FB > Twit

Autor

galet@world

Član broj: 81985
Poruke: 1076
*.adsl-1.sezampro.yu.

+3 Profil

Re: Teorija Relativnosti

^{28.10.2008. u 08:12 - pre 200 meseci}

Citat:

tomkeus:Na ovu situaciju ne možeš da primeniš STR zato što referentni sistem vezan za trkače nije inercijalan i na osnovu STR ne možeš da kažeš šta se u njemu dešava za vreme ubrzavanja trkača. Postavio si naopako pitanje. Ti si kretanje trkača definisao u odnosu na inercijalni referentni sistem vezan za posmatrače trke i ono što ti trebaš da pitaš je koliko je rastojanje između trkača u sopstvenom referentnom sistemu. Na to pitanje ti STR ne može dati odgovor.
edit: Da ovde ne bude zabune, hteo sam da kažem da ti STR može reći da u trenutku kada trkači prestanu da ubrzavaju rastojanje u njihovom sopstvenom referentnom sistemu će biti 100/k metara, ali ti ne može reći šta se dešavalo za vreme ubrzanja, tj. zašto se to rastojanje uvećalo za vreme ubrzavanja.

Opet nevešte relativističke eskivaže.
Postavio sam naopako pitanje!!! Bravo. Neka pitanja relativistima zaista ne odgovaraju jer ne znaju odgovor.
Pitanje jednostavnije i ispravnije ne može biti.
Oba trkača su non stop pod jednakim uslovima - a zašto su po bilo kojoj teoriji posledice različite?

Kako mogu njihova ubrzanja, brzine i pređeni putevi biti različiti za bilo koga i u bilo kom referentnom sistemu
uključujući i njihov kad za to nema nikakvog uzroka?

Kažeš da se u referentnom sistemu trkača po prestanku ubrzanja njihovo rastojanje uvećalo. Zašto?
A u referentnom inercijalnom sistemu ostalih promatrača se to rastojanje umanjilo. Zašto?
(ova dva pitanja promatraj potpuno samostalno i nezavisno jedno od drugog)
Sve logički "biseri" jedan do drugog.

Po tebi identični uslovi daju različite posledice. Zaista fascinantno odsustvo logike.

_{[Ovu poruku je menjao galet@world dana 28.10.2008. u 10:32 GMT+1]}

0

Sprečo
penzioner

Član broj: 27004
Poruke: 1229
92.36.132.*

+33 Profil

Re: Teorija Relativnosti

^{28.10.2008. u 12:11 - pre 200 meseci}

Dane, među "relativistima" je mnogo osoba koje mogu puno zapamtiti (naučiti) i to reprodukovati (imaju veliko znanje, "kompjutersko znanje"). Ne očekuj od većine takvih da imaju i umenje (sposobnost uočavanja i zaključivanja). U ophođenju sa "relativistima" moramo imati ogromno strpljenje (kao sa malom djecom) i postepeno ih voditi putovima ka vlastitoj spoznaji. Samo polako i strpljivo, vodi im misao od najprostijeg ka složenijem.

0

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8700
*.dynamic.sbb.rs.

+2801 Profil

Re: Teorija Relativnosti

^{28.10.2008. u 13:59 - pre 200 meseci}

Citat:

galet@world: Opet nevešte relativističke eskivaže.
Postavio sam naopako pitanje!!! Bravo. Neka pitanja relativistima zaista ne odgovaraju jer ne znaju odgovor.
Pitanje jednostavnije i ispravnije ne može biti.

Specijalna se valjda ne bavi ubrzanim sistemima, ali to ne znaci da ovo konkretno pitanje nema konkretan relativisticki odgovor. Odgovor na ovo pitanje moze dati opsta teorija relativnosti. No, ta teorija je slozenija.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

0

tomkeus

Član broj: 40478
Poruke: 503
*.eunet.rs.

+6 Profil

Re: Teorija Relativnosti

^{28.10.2008. u 14:52 - pre 200 meseci}

Citat:

galet@world: Opet nevešte relativističke eskivaže.

Nije nikakva eskivaža. Obrati pažnju kako si definisao problem. Ti si rekao da su trkači na rastojanju na 100m jedan od drugog na početku. Pre nego što krenu da trče trkači i publika dele isti referentni sistem i nema nikakvog problema, i publika i trkači kažu da su na rastojanju od 100m. E onda kreću da trče i obrati pažnju šta si ti rekao: trče jednakim ubrzanjima određeni vremenski interval i onda nastave da se kreću istim brzinama. Sve ove izjave se odnose na referentni sistem posmatrača trke koji je inercijalan i nije problematičan sa stanovišta STR. Ovaj tvoj iskaz se odnosi samo na referentni sistem posmatrača, a ti si u tom iskazu postavio kretanje tako da rastojanje između trkača u referentnom sistemu posmatrača trke uvek bude 100m. Jednostavno, tvrdnja "trkači su u referentnom sistemu posmatrača trke na rastojanju 100m" je tautologija. Pitanje na koje odgovor nije trivijalan je koliko je rastojanje u sistemu u kome trkači miruju? STR ti može dati odgovor na to pitanje kada trkači prestanu da ubrzavaju, ali ti neće dati odgovor na to šta se dešavalo za vreme ubrzavanja, tj. zašto se za vreme ubrzavanja rastojanje u sopstvenom referentnom sistemu trkača povećalo sa 100m na

m jer taj referentni sistem nije inercijalan u toku ubrzavanja. Za to moraš da pitaš opštu teoriju relativnosti.

0

Sprečo
penzioner

Član broj: 27004
Poruke: 1229
92.36.144.*

+33 Profil

Re: Teorija Relativnosti

^{28.10.2008. u 17:00 - pre 200 meseci}

Tomkeus, slažeš li se da prethodna "korekcija" zavisi od odnosa brzina n = c/v , a ne zavisi od toga kolike su te brzine (koliki su intenziteti brzina c i v), te to "povećanje" 100m možemo lijepo proučiti i na primjeru ISR za c = 0,5m/s i v = 0,3m/s , jednako valjano kao da ga proučavamo i na ISR i brzine c = 300 000km/s i v = 180 000km/s ???
Nedeljko, V. J. Žigman u svom udžbeniku STR lijepo je objasnila "usputne" ISR.

_{[Ovu poruku je menjao Sprečo dana 28.10.2008. u 19:31 GMT+1]}

0

tomkeus

Član broj: 40478
Poruke: 503
*.eunet.rs.

+6 Profil

Re: Teorija Relativnosti

^{29.10.2008. u 03:17 - pre 200 meseci}

Nebitno je kolike su brzine. To zavisi od sistema jedinica koji koristimo. Npr. ljudi koji rade opštu teoriju relativnosti uzimaju sistem jedinica u kome je c=1 (bezdimenziono) tako da u tom sistemu jedinica dužina i vreme imaju iste dimenzije tako da što se mene tiče možeš da uzmeš i c=1.

Nisam još uvek pažljivo pročitao one strane, jer pažljivo čitanje zahteva vremena, ali jedno ću ti reći: u principu se nisi setio ničega što nije predlagano od mase najeminentnijih figura perioda između 1880. godine i negde 1907-1908. U principu bilo je na hiljade različitih predloga o tome kako da se razreše problemi koji su bili prisutni u fizici još od vremena kada je Džejms Bredli uočio problem sa aberacijom zvezda 1728. godine. Argumentacija za i protiv je bila ogromna i iz svega toga se postepeno rodila STR ovakva kakvu danas znamo. Pošto je istorijat svega toga zamašan sa gomilom eksperimenata, a materijal je na engleskom (mada sam dosta originalnih radova pogledao na francuskom i pomalo na nemačkom, pošto nemački vrlo slabo razumem), a meni se čini da si negde pominjao da imaš problema sa engleskim to će mi otežati stvari. Trebaće mi malo više vremena da sastavim sve to u jedan koliko toliko suvisli dokument gde ću pokušati da ti dam istoriju problema i zašto su predlozi kao onaj koji si ti napravio odbačeni.

0

Sprečo
penzioner

Član broj: 27004
Poruke: 1229
92.36.130.*

+33 Profil

Re: Teorija Relativnosti

^{29.10.2008. u 04:21 - pre 200 meseci}

Tomkeus, engleski pojma nemam, francuski učio i već zaboravio, ovo što znam također zaboravljam (senilim) i svaki dan sam sve bliži da spoznam šta je "nirvana". Zato te molim ne troši svoje vrijeme da me bilo čemu poučiš, uputiš, uvjeriš (razuvjeriš). Moji dani su izbrojani i meni to ne treba. Ovo što pišem (http://mimo_2.bloger.hr/) želim ostaviti mlađim, promućurnim, koji će znati to iskoristiti.
Tvoja prethodna primjedba za n = c/v , govori kako nije bitan izbor jedinica, a ja tome dodajem: Koje jedinice koristiš u mjernom broju za "izmjerenu dužinu", moraš iste te jedinice koristiti i za mjerne brojeve brzina c i v ( u "relativističkom faktoru"). Također, tvoja prethodna primjedba ne uklanja valjanost mog pitanja (na koje si izbjegao direktan odgovor).
Edit: A kada je c = 1 obradio sam ovdje još 2005. godine.

_{[Ovu poruku je menjao Sprečo dana 29.10.2008. u 14:24 GMT+1]}

0

Sprečo
penzioner

Član broj: 27004
Poruke: 1229
92.36.168.*

+33 Profil

Re: Teorija Relativnosti

^{29.10.2008. u 06:10 - pre 200 meseci}

Po ovom pitanju

Citat:

Nikola Tesla nije nikakav autoritet po pitanju elektrodinamike.

ste (Tomkeus i M. Milošević) jako "površni".
Čovjek nemože biti dobar praktičar (u ovoj oblasti) ako ne poznaje suštinu ("elektrodinamiku"). I nije to "navijanje" za svoga!

0

zzzz
milan kecman
bluka

zzzz
Član broj: 11810
Poruke: 2164
92.241.128.*

+197 Profil

Re: Teorija Relativnosti

^{29.10.2008. u 11:28 - pre 200 meseci}

tomkeus:
... Oko elektrona koji se kreće, istina pored električnog postoji i magnetno polje, ali elektromagnetizam je linearna interakcija i elektromagnetno polje ne interaguje samo sa sobom tako da to što u referentnom sistemu u odnosu na koji se elektron kreće postoji magnetno polje ne može da zakoči elektron.

Samo da razjasnimo ovo:Da li je magnetno polje, koje spominješ, stalnog intenziteta ili raste?Ako se magnetno polje mijenja, da li ono indukuje struju?Da li ta indukovana struja ima magnetno polje?(Ili da idemo pročitati šta kaže Tesla?)

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

0

zzzz
milan kecman
bluka

zzzz
Član broj: 11810
Poruke: 2164
92.241.128.*

+197 Profil

Re: Teorija Relativnosti

^{29.10.2008. u 11:40 - pre 200 meseci}

Ne postoji bočna masa niti bilo šta slično, ..

Slažem se.
Ali kada ubrzavamo elektron opažamo da sporije ubrzava kad mu je brzina veća.Relativnost to tumači porastom mase .
Ali istovremeno možemo djelovati i bočno novim el. poljem.Ovdje nema takvog
otpora ubrzavanju.Zašto?Ovo je eksperimentalno zapažanje.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

0

Sprečo
penzioner

Član broj: 27004
Poruke: 1229
92.36.174.*

+33 Profil

Re: Teorija Relativnosti

^{29.10.2008. u 13:35 - pre 200 meseci}

Citat:

Ako se magnetno polje mijenja, da li ono indukuje struju?Da li ta indukovana struja ima magnetno polje?(Ili da idemo pročitati šta kaže Tesla?)

Ne koristim izraz "indukuje struju", već indukuje ("samoindukcija") elektromagnetno polje suprotnog dejstva.
Edit: Tomkeus se davno izjasnio da nema promjene mase sa promjenom brzine kretanja tijela (njemu te stvari nemoj napominjati).

0

galet@world

Član broj: 81985
Poruke: 1076
*.adsl-a-1.sezampro.yu.

+3 Profil

Re: Teorija Relativnosti

^{30.10.2008. u 14:27 - pre 199 meseci}

Citat:

Nedeljko: Specijalna se valjda ne bavi ubrzanim sistemima, ali to ne znaci da ovo konkretno pitanje nema konkretan relativisticki odgovor. Odgovor na ovo pitanje moze dati opsta teorija relativnosti. No, ta teorija je slozenija.

Citat:

tomkeus: Nije nikakva eskivaža. Obrati pažnju kako si definisao problem. Ti si rekao da su trkači na rastojanju na 100m jedan od drugog na početku. Pre nego što krenu da trče trkači i publika dele isti referentni sistem i nema nikakvog problema, i publika i trkači kažu da su na rastojanju od 100m. E onda kreću da trče i obrati pažnju šta si ti rekao: trče jednakim ubrzanjima određeni vremenski interval i onda nastave da se kreću istim brzinama. Sve ove izjave se odnose na referentni sistem posmatrača trke koji je inercijalan i nije problematičan sa stanovišta STR. Ovaj tvoj iskaz se odnosi samo na referentni sistem posmatrača, a ti si u tom iskazu postavio kretanje tako da rastojanje između trkača u referentnom sistemu posmatrača trke uvek bude 100m. Jednostavno, tvrdnja "trkači su u referentnom sistemu posmatrača trke na rastojanju 100m" je tautologija. Pitanje na koje odgovor nije trivijalan je koliko je rastojanje u sistemu u kome trkači miruju? STR ti može dati odgovor na to pitanje kada trkači prestanu da ubrzavaju, ali ti neće dati odgovor na to šta se dešavalo za vreme ubrzavanja, tj. zašto se za vreme ubrzavanja rastojanje u sopstvenom referentnom sistemu trkača povećalo sa 100m na

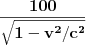
m jer taj referentni sistem nije inercijalan u toku ubrzavanja. Za to moraš da pitaš opštu teoriju relativnosti.

Verovatno će biti mnogo jasnije ako detaljnije razmislimo šta je kontrakcija dužine sama po sebi
nevezano za bilo kakvu teoriju.

Navedimo pre toga aksiom o jednakosti:

Jednake prirodne pojave (procesi) pod jednakim uslovima događaju se jednako.

A sada da odgovorimo na pitanje – šta je kontrakcija dužine.

Kontrakcija dužine je međusobno približavanje tačaka te dužine po bilo kakvoj zakonitosti
uz uslov da dužina ostaje neprekinuta i da je kontrahirana dužina manja od početne.

Specijalan slučaj kontrakcije dužine je proporcionalna kontrakcija dužine.

Proporcionalna kontrakcija dužine je približavanje tačaka te dužine prema nekoj tački koja
može biti bilo gde unutar te dužine ili bilo gde izvan te dužine na pravoj na kojoj leži ta
dužina.

Nazovimo tu tačku centar kontrakcije.

Približavanje tačaka dužine centru kontrakcije proporcionalno je njihovoj udaljenosti od
centra kontrakcije.

Ovo je samo jedan specijalan slučaj kontrakcije dužine jer kontrakcija dužine se može ostvariti i
sa drukčijim međusobnim približavanjem tačaka te dužine, ali osnovni rezultat
kontrakcije dužine je taj da je kontrahirana dužina manja od početne bez obzira na koji
način je ostvarena kontrakcija.

Kod proporcionalne kontrakcije dužine ta dužina kontrahira tako što tačke koje su udaljenije
od centra kontrakcije prelaze veća rastojanja u odnosu na centar kontrakcije od onih tačaka
koje su bliže tom centru. Dakle, kod proporcionalne kontrakcije dužine ni jedna tačka te
dužine nije pod jednakim uslovima jer su im odstojanja od centra kontrakcije različita.

Prema tome proporcionalna kontrakcija dužine, sama po sebi, je pojava koja isključuje
jednakost uslova.

To isto se odnosi i na bilo kakvu drukčiju kontrakciju dužine. Činjenica da je kontrahirana
dužina kraća od početne ne može se ni po kakvoj teoriji ostvariti ako su uslovi za
svaku tačku te dužine jednaki jer bi to bila negacija aksioma o jednakosti.

NAPOMENA:

Postojanje ili nepostojanje promatrača u bilo kom referentnom sistemu ne menja ovu
analizu niti ima bilo kakvog uticaja na nju.

0

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8700
195.222.97.*

+2801 Profil

Re: Teorija Relativnosti

^{30.10.2008. u 21:33 - pre 199 meseci}

Off topic:

Neka su referentni sistemi S i S' povezani relacijama

,

(događaj koji se u S desio na mestu x u trenutku t se u sistemu S' se desio na mestu x' u trenutku t').

Ako se neka tačka kreće u sistemu S po zakonu x=ut i u dva trenutka t₁ i t₂ se tačka "palila" (recimo da je to sijalca) na mestima x₁=ut₁ i x₂=ut₂. Ti događaji su se u sistemu S' desili u trenucima t'₁=(ru+s)t₁ i t'₂=(ru+s)t₂ na mestima x'₁=(pu+q)t₁ i x'₂=(pu+q)t₂. Dakle, od jednog do drugog događaja tačka je u sistemu S' prešla put (pu+q)(t₂-t₁) za vreme (ru+s)(t₂-t₁), odnosno, kreće se vrzinom

. Sada primeniti to na Lorencove transformacije i izračunati u' u slučaju u=c.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

0

galet@world

Član broj: 81985
Poruke: 1076
*.adsl-a-1.sezampro.yu.

+3 Profil

Re: Teorija Relativnosti

^{01.11.2008. u 13:36 - pre 199 meseci}

Pojam vremena t' je nedokaziva relativistička izmišljotina, ali trenutno nije tema pa nek
stoji.

U ovoj računici nedostaje još jedna sijalica na odstojanju od 100 m.

t'₁ = r(ut₁ - 100) + st₁ i t'₂ = r(ut₂ - 100) + st₂ pa je opet t'₂ - t'₁ = (ru+s)(t₂-t₁)
x'₁ = p(ut₁ - 100) + qt₁ i x'₂ = p(ut₂ - 100) + qt₂ te je put: x'₂ - x'₁ =(pu+q)(t₂-t₁)

Prema tome i ova sijalica ima istu brzinu. Ako bilo šta činimo ili primenjujemo na jednoj sijalici
pa to isto uradimo i sa drugom sijalicom – razmak među njima se neće menjati jer je to u
saglasnosti sa aksiomom o jednakosti.

0

Sprečo
penzioner

Član broj: 27004
Poruke: 1229
92.36.132.*

+33 Profil

Re: Teorija Relativnosti

^{02.11.2008. u 06:11 - pre 199 meseci}

Nedeljko, naučio sam (na fruli) svirati "moravac", te igrajmo po mojoj svirci: Mislim da nam definicija ISR, međusobnog relativnog kretanja brzinom v dva objekta ("kruto" za njih vežimo K i K') nije sporna. Na početku posmatranja, mjerenja, računanja, K i K' se poklapaju (koordinatni počeci u tački P).
Na kraju posmatranja relativnog kretanja brzinom v ( uslovno imenujmo K' da se kretao u odnosu na K , tj koordinatni početak K' kretao se u odnosu na P po x-osi brzinom v) istekom vremenskog intervala t imamo dužinu PP'' = vt. Na početku posmatranja iz tačke P širio se i sferni val (u svima pravcima i smjerovima brzinom c > v > 0 , neovisno od brzine kretanja izvora i neovisno od brzine kretanja prijemnika), te je istekom vremenskog intervala t dospio na udaljenost od tačke P po zakonu puta PA = ct = x.
Neka je n = c/v = 5/3 = ct/vt = PA/PP'' . Izračunajmo Lorentzove dužine: x, x', vt, vt' , za neki konkretan primjer "izmjerene dužine" (bilo koje).
Da mi ne bi pričao priče o početnoj tački P uzmi da je ta tačka na tvom radnom stolu, a za intenzitete brzina uzmi bilo koje vrijednosti ("inercijalne") datog omjera (jer vrijednost "relativističkog faktora" za zadano n će biti 4/5).
Da bi propratili i veoma lijep pristup D. Gaćeša uzmimo da je navedenih 100m "izmjerena dužina" (u mirovanju 2l_0), te da se "pokretni posmatrač" (koordinatni početak K') nalazi u njenoj sredini.

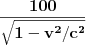
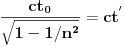
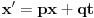
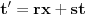
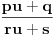
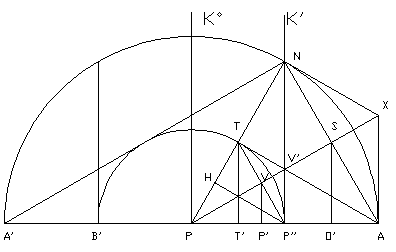Molim da ne zamjerite što sam "plasirao" sliku omjera n = c/v = 2/1 (za ovaj omjer n = 2/1 , vrijednost "relativističkog faktora" će biti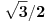

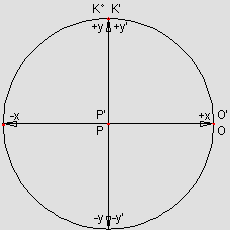) umjesto omjera n = 5/3.
Evo i slike za omjer n = 5/3 i vrijednost "relativističkog faktora" 4/5 pravi omjer, ali sa drugačijim obilježavanjem tačaka.

_{[Ovu poruku je menjao Sprečo dana 02.11.2008. u 08:13 GMT+1]}

Prikačeni fajlovi

Sve dužine.gif

Sve dužine.gif - 3.19k

0

Sprečo
penzioner

Član broj: 27004
Poruke: 1229
92.36.136.*

+33 Profil

Re: Teorija Relativnosti

^{03.11.2008. u 06:34 - pre 199 meseci}

„Relativisti“, Dane vam je postavio čisto, lijepo i konkretno pitanje:
Imate dužinu AC = 100m = A'C'. Na početku posmatranja (računanja, čega god hoćete) oba koordinatna početka (K° i K') su u sredini te dužine u tački P identično P'. Dužine (i „lijevo“ i „desno“ su jednake: AP = AP' = PC = P'C' = 50m. Imate početnu sliku:

. „Relativisti“, pomjerite tu dužinu AC = A'C' = 100m, brzinom (kojom god želite) v = c/n , tako da je nakon pomjeranja PP' = vt. Kažite (izračinajte i nacrtajte) šta se tu „skratilo“, za koliko, u odnosu na koju tačku, šta je sa krajevima dužine A'C' (jesu li se „približili međusobno“ ili nisu, jesu li prešle istu razdaljinu – kao središnja tačka duži - ili nisu)?! Konkretne brojke i konkretan crtež – molim. Nema priče o „crnim rupama“, paralelnim svjetovima, česticama i akceleratorima , samo ISR, brzine, dužine, vrijeme, ...

Prikačeni fajlovi

sl-001.gif - 1.3k

0

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8700
*.dynamic.sbb.rs.

+2801 Profil

Re: Teorija Relativnosti

^{03.11.2008. u 10:33 - pre 199 meseci}

Citat:

galet@world: U ovoj računici nedostaje još jedna sijalica na odstojanju od 100 m.

Ne nedostaje nikakva sijalica, jer se racun odnosi na odredjeni misaoni eksperiment (koji bi ti da promenis) i koji ima samo jednu sijalicu. No, kada promenis misaoni eksperiment, onda se menja i racun koji se na njega odnosi.

Racun koji sam izlozio je izvodejenje formula za transformaciju brzine pri prelasku izmedju dva referentna sistema povezana linearnim transformacijama, kakve god one bile. Na kraju sam naveo poseban slucaj transformacije brzine c kada su te transformacije Lorencove. Da li ce neko prihvatiti te transformacije ili ne, u to pitanje nisam ulazio.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

0

tomkeus

Član broj: 40478
Poruke: 503
*.eunet.rs.

+6 Profil

Re: Teorija Relativnosti

^{03.11.2008. u 10:54 - pre 199 meseci}

Citat:

Sprečo:
Tvoja prethodna primjedba za n = c/v , govori kako nije bitan izbor jedinica, a ja tome dodajem: Koje jedinice koristiš u mjernom broju za "izmjerenu dužinu", moraš iste te jedinice koristiti i za mjerne brojeve brzina c i v ( u "relativističkom faktoru"). Također, tvoja prethodna primjedba ne uklanja valjanost mog pitanja (na koje si izbjegao direktan odgovor).
Edit: A kada je c = 1 obradio sam ovdje još 2005. godine.

Lorencov bust

zaista zavisi samo od odnosa v/c tako da ako gledaš samo njega apsolutno su nebitne numeričke vrednosti u bilo kom sistemu jedinica, ali kada bustuješ neki vektor, sam vektor (npr. ct-koordinata) i te kako zavisi od numeričkih vrednosti u svakom sistemu jedinica. Jednom rečju, stavljanjem, npr. c=1m/s ti skaliraš ili dužinu ili vreme što nije dozvoljeno jer fizika nije invarijantna na promenu skale. Dakle, ako ti se numerička vrednost c=300000km/s ne sviđa, uzmi koju god hoćeš, ali makni km/s, tj. promeni jedinice. Mislim, možemo mi da se igramo sa c=50km/h do određene granice, ali ako probamo nešto konkretno da izračunamo, npr. šta se dešava sa običnom dipolnom antenom dobićemo besmislene rezultate (ovo važi generalno, za bilo koje svojstvo koje uključuje električnu i magnetnu permeabilnost materijala).

Citat:

zzzz:Relativnost to tumači porastom mase .

Možda u nekoj knjizi od pre WWII (mada se većina naučnopopularnih i sve srednjoškolske knjige tako još uvek pišu). Stvar je prosto u različitoj kinematici koja uzrokuje darugačije ponašanje kinetičke energije. Danas se masa u teorijskoj fizici definiše kao jedan od dva kvantna broja (drugi je spin) koji karakteriše ireducibilne reprezentacije Poenkareove grupe i konkretno je povezana sa sistemom mirovanja čestice.

Citat:

zzzz: tomkeus:
Samo da razjasnimo ovo:Da li je magnetno polje, koje spominješ, stalnog intenziteta ili raste?Ako se magnetno polje mijenja, da li ono indukuje struju?Da li ta indukovana struja ima magnetno polje?(Ili da idemo pročitati šta kaže Tesla?)

U čemu to polje indukuje struju?

0

Milan Milosevic

Član broj: 67
Poruke: 932
79.101.180.*

+31 Profil

Re: Teorija Relativnosti

^{03.11.2008. u 12:41 - pre 199 meseci}

Ogovor na galet@world pitanje sta se i kako se skracuje dali jos ranije, ali ocito niste zadovolji kad stalno iznova postavljate isto pitanje na koje ce te dobijeti uvek isti odgovor.

0

galet@world

Član broj: 81985
Poruke: 1076
*.adsl-1.sezampro.yu.

+3 Profil

Re: Teorija Relativnosti

^{03.11.2008. u 13:32 - pre 199 meseci}

Citat:

Nedeljko: Ne nedostaje nikakva sijalica, jer se racun odnosi na odredjeni misaoni eksperiment (koji bi ti da promenis) i koji ima samo jednu sijalicu. No, kada promenis misaoni eksperiment, onda se menja i racun koji se na njega odnosi.

Očigledno je ko šta menja i zašto menja. Pitanje se odnosilo na kontrakciju dužine, a ne
na iznošenje detalja bilo kakve teorije uz pomoć "misaonih" (besmislenih) eksperimenata.

Nedvosmisleno je dokazano da stoji tvrdnja:

Kontrakcija dužine i jednakost uslova se međusobno isključuju

To je definitivno jedan od neoborivih logičkih udaraca protiv STR.

0

elitemadzone.org :: MadZone :: Teorija Relativnosti
(Zaključana tema (lock), by Tyler Durden)
Strane: << < .. 86 87 88 89 90 91 92 93 94 95 ... Dalje > >>

[ Pregleda: 468991 | Odgovora: 2583 ] > FB > Twit

Srodne teme

16.01.2003. teorija algoritama?
11.01.2010. Gravitacija - Kvantna teorija ...
08.05.2003. identifikacija broja (sa kompjuterom)
19.05.2003. verovatnoća i statistika-literatura
11.02.2004. Maturski rad - teorija relativnosti
16.01.2009. Knjiga za teoriju relativnosti
03.10.2005. Teorija relativnosti - pod lupom, (alternativno t..
04.04.2005. dopplerov efekt i hubbleov zakon
30.12.2005. teorija skupova-kardinalni brojevi
03.01.2006. rotacijski luk - teorija

Navigacija

Lista poslednjih: 16, 32, 64, 128 poruka.