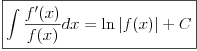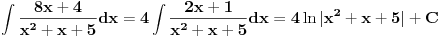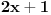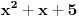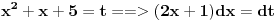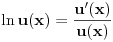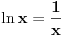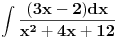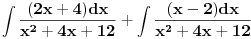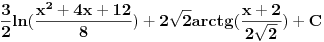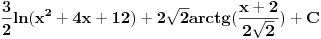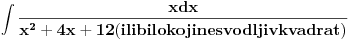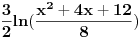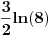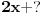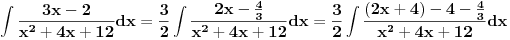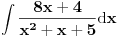
Rešavanje (neki delovi su mi komplikovani za tex, izvinjavam se):
"Odvajam" Int8xdx/(x^2+x+5) + Int4dx/(x^2+x+5)
Polinom x^2+x+5 svodim na oblik t^2 + 1 (zbog arctg(t)) pa se ispod razlomačke crte dobija redom
(x^2+x+1/4)^2 + 19/4 = 19/4 ( ((x+1/2)/(sqrt19/2))^2 + 1 )
i uglavnom posle sređivanja i "izbacivanja" koeficijenta ispred integrala, ostaje
((2x+1)/sqrt19)^2 + 1
Uzimam smenu t = (2x+1)/sqrt19 (da li je ispravno da za prvi integral tj
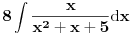 uzmem tu smenu?)
uzmem tu smenu?)t=
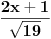
dx=
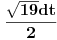
x=
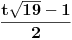
Dalje sve ide dobro i dobije se na kraju izmedju ostalog
8Int tdt/t^2 + 1
koji ja resavam na sledeci nacin
smena: s=t^2+1 (da li je u redu?)
ds=2tdt
ds/2=tdt
i time svodim na oblik 4Int ds/s sto je jednako 4ln(s), to je dalje jednako 4ln(t^2+1) = 4ln((4x^2+4x+20)/19) - primetiti da se deljenjem brojioca sa 4 dobija x^2+x+5
i tu stizemo do problema jer u resenju pise 4ln(x^2+x+5) (ostatali integrali u resenju se oduzmu medjusobno pa je ovo celo resenje, i ja dobijem da moze da se oduzme).
Pretpostavljam da gresim negde u smeni.
Da li bi neko mogao da uradi ovaj zadatak ili da mi ukaze na gresku?
Hvala puno.




 Integrali racionalnih funkcija
Integrali racionalnih funkcija