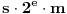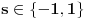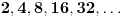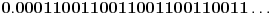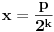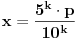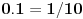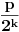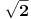@str-es
Brojevi u pokretnom zarezu se matematicki gledano pamte u obliku
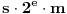
, gde je
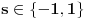
,

neki ceo broj (opseg je ogranicen),a

broj koji nije manji od nule, a manji je od

. U principu nije manji ni od
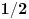
ali moze da bude ako je broj blizak nuli (preciznije, ako

uzima najmanju vrednost iz dozvoljenog opsega) i tada se zove subnormalnim jer se belezi manji broj znacajnih binarnih cifara, ali se u racunu ponasa kao najobicniji realan broj. No, broj

se belezi sa fisknim brojem binarnih cifara, koji zavisi od tipa podatka koji se koristi (u jezicima C/C++ float, double ili long double) i to je ono sto je ovde od esencijalne vaznosti. Dakle,
Brojevi u pokretnom zarezu se beleze sa konacnim brojem binarnih cifara.
E, sad, posto niti jedan potpun stepen broja

(dakle, broj poput
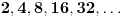
) nije deljiv sa 10, u opstem slucaju konverzija iz dekadnog zapisa u binarni se ne moze obaviti tacno, vec samo priblizno. Preciznije, postoje brojevi koji u dekadnom sistemu imaju konacan zapis, a u binarnom sistemu beskonacan zapis. Takav je recimo broj 0.1 koji u dkadnom sistemu ocigledno ima konacan zapis, ali u binarnom ima beskonacan periodicni zapis koji glasi
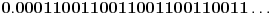
Iz tog razloga se broj 0.1 ne moze prikazati tacno nijednim sistemom zasnovanim na zapisima konacnog broja binarnih cifara, vec samo priblizno. Kada u jeziku C++ napises nesto poput
Code:
double x = 0.1;
cout << x << endl;
promenljiva x ce dobiti vrednost koja je priblizno jednaka 0.1, ali joj nije jednaka. Medjutim, na ekranu ce biti prikazan broj 0.1 jer se ispis vrsi na svga nekoliko decimala, pa je odstupanje dovoljno malo da se prilikom konverzije u dekadni brojni sistem (u kome ce broj biti prikazan na ekranu) vrsi zaokruzivanje na 0.1.
Medjutim, broj 10 je deljiv brojem 2, pa svaki broj koji ima konacan binarni zapis ima i konacan dekadni zapis. Zaista, ako neki broj

ima konacan binarni zapis, on mora biti oblika
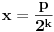
za neki ceo broj

i prirodan broj

. Medjutim, tada je
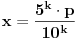
,
pa svakako ima i konacan dekadni zapis. Za razliku od toga, broj
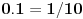
se ne moze prikazati u obliku
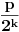
jer koliko god puta ga mnozio dvojkom, neces pokratiti onu desetku dole i dobiti ceo broj.
Stoga je obrnuta konverzija (iz binarnog sistema u dekadni) u principu moguca, pa se moze prikazati na ekranu u dekadnom sistemu sta je tacno racunar zapamtio.
Matematicki, da bi "izvukao" dekadne cifre iz broja x koji ima konacan binarni zapis, trebao bi da izvrsis sledecu proceduru
Code:
while (x>0) {
cout << floor(x*10);
x = 10*x - floor(10*x);
}
cout << endl;
Medjutim, ni tada neces dobiti tacan rezultat (bar ne u opstem slucaju) jer ova procedura koristi racunske operacije (kao sto je mnozenje sa 10) koje se takodje obavljaju samo priblizno u racunaru. Stoga se procedura koja ispisuje tacno u dekadnom sistemu sta je tacno zapamceno u promenljivoj tipa float, double ili long double mora pisati daleko pazljivije.
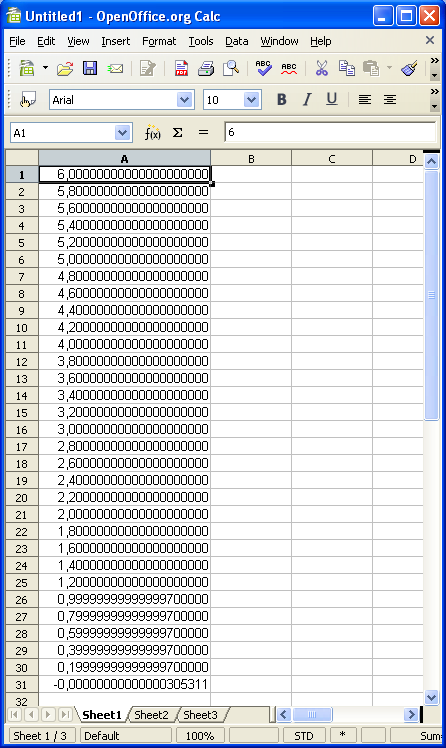
Ako te zanima sta se tacno dobija u promenljivama tih tipova kada pokusas da smestis u njih jedinicu, pa izvrsis delenje sa 10, evo, za tebe sam izracunao tacne vrednosti memorisanih brojeva:

Na kraju, zasto je 0.2-0.2=0. Pa zato sto, bez obzira sto je reprezentacija broja 0.2 u memoriji racunara samo priblizna, ona je (u istom tipu) uvek ista, pa kada istu velicinu (kakva god da je) oduzmes od iste, svakako da treba da dobijes nulu.
[Ovu poruku je menjao Nedeljko dana 23.07.2008. u 11:16 GMT+1]
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.




 Novi excel bug? 0=-3,1E-15?
Novi excel bug? 0=-3,1E-15?