Hajde da citiram nesto iz Landau-a.
''Skrecemo paznju na cinjenicu da se u kvantnoj mehanici pri finitnom kretanju cestica moze nalaziti i u onim oblastima prostora u kojima je

. Verovatnoca nalazenja cestice, iako i tezi brzo ka nuli sa povecanjem rastojanja u dubini te oblasti, ipak je razlicita od nule za sva konacna rastojanja''
''Smatracemo da fja
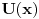
za
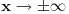
tezi ka konacnim granicama (ali nikako ne mora biti monotona fja). Granicu
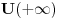
uzecemo za pocetak racunanja energije [tj. stavicemo
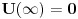
], a
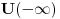
obelezicemo sa
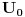
i smatracemo da je
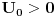
. Diskretni spektar se nalazi u oblasti takvih vrednosti energije za koje cestica ne moze preci u beskonacnost (vrlo daleko). Zbog toga energija mora biti manja od obe granice
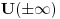
, tj. mora biti negativna

''
Po meni tvoj zakljucak sledi iz ova dva citata Landau-a. Jesam li u pravu? Naravno ne mora se uzeti ovaj uslov
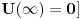
i to ce nas tacno prebaciti u ono sto si ti napisao
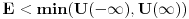
. Jel tacno?
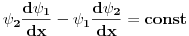
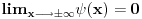
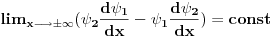
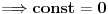
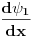 i
i 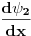 mogu da divergiraju?
mogu da divergiraju?