[es] - Kako koristenjem brojeva 5 2 3 3 dobiti 100

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Kako koristenjem brojeva 5 2 3 3 dobiti 100

^{14.07.2008. u 22:24 - pre 204 meseci}

Citat:

adnanK: Dakle, ne smije se koristiti stepenovanje, vec samo osnovne racunske operacije, tj, + - x i /. Takodje svaki broj smijete koristiti samo jednom.

Ja cu definisati

kao

gde je

sabiranje brojeva, a

neka osnovna operacija ovako definisana

http://www.svijetfizike.com/

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dynamic.sbb.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Kako koristenjem brojeva 5 2 3 3 dobiti 100

^{14.07.2008. u 22:48 - pre 204 meseci}

S ova

broja i

operacije može se dobiti najviše

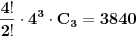
različitih rezultata (prvi činilac predstavlja broj mogućih rasporeda ova četiri broja, pri čemu delimo sa

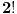
jer se dva puta pojavljuje isti broj; drugi činilac prebraja operacije koje se mogu udenuti između određenog rasporeda datih brojeva; treći činilac je

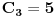
, Katalanov broj, i on uračunava zagrade). Naravno, stvarni broj različitih rezultata je dosta manji (pre svega, neki od dobijenih izraza su ekvivalentni, a i možda i neki drugi daju isti rezultat), ali i ovo je dovoljno da se začas (računarom) testira može li se dobiti traženi broj. Štaviše, program dole (pisan u programskom paketu Mathematica) pronalazi sva rešenja: ima ih ukupno

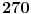
(računajući i

), i među njima nema broja

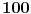
(štaviše, najveći rezultat je

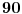
, a najmanji

Code:
Module[{Operacije, Permutacije, i, j, k, p, a, b, c, d, op1, op2,
  op3},
Resenja = {};
Operacije = {"+", "-", "*", "/"};
Permutacije = Permutations[{"5", "2", "3", "3"}];
For[i = 1, i <= 4, i++,
  For[j = 1, j <= 4, j++,
   For[k = 1, k <= 4, k++,
    For[p = 1, p <= Length[Permutacije], p++,
     a = Permutacije[[p, 1]];
     b = Permutacije[[p, 2]];
     c = Permutacije[[p, 3]];
     d = Permutacije[[p, 4]];
     op1 = Operacije[[i]];
     op2 = Operacije[[j]];
     op3 = Operacije[[k]];
     Resenja = Join[Resenja, {
        ToExpression[
         StringJoin["((", a, op1, b, ")", op2, c, ")", op3, d]],
        ToExpression[
         StringJoin["(", a, op1, "(", b, op2, c, "))", op3, d]],
        ToExpression[
         StringJoin["(", a, op1, b, ")", op2, "(", c, op3, d, ")"]],
        ToExpression[
         StringJoin[a, op1, "((", b, op2, c, ")", op3, d, ")"]],
        ToExpression[
         StringJoin[a, op1, "(", b, op2, "(", c, op3, d, "))"]]
        }]
     ]
    ]
   ]
  ];
Resenja = Union[Resenja]
]

Onda mi je palo na pamet da je autor zadatka možda prihvata i (unarnu) operaciju negacije. No, svaki tako dobijen broj već bi se morao nalaziti na dobijenom spisku, eventualno sa suprotnim znakom. Kako smo već konstatovali da je najmanji broj koji smo dobili

, ni s ovim dodatkom ne možemo premašiti

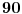
. Dodajmo samo da se u ovom slučaju dostiže

različitih rešenja.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu