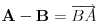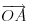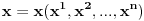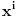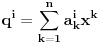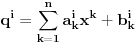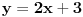[es] - Afini prostori???

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

^{09.07.2008. u 22:10 - pre 218 meseci}

Ima li razlike izmedju afinih i linearnih vektorskih prostora? I ako ih ima koje su razlike? Mislim da bi trebalo strogo reci da je fja

afina, dok je

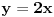linearna fja. Ali naravno to niko ne radi. Po literaturi sam nasao da tenzore zovu i afinori.
Voleo bih da malo rascistim stvari oko ove terminologije! Pa ako neko zna nesto o ovome bio bih mu zahvalan da i napise to!:) Mislim da je moguce da su afini prostori siri termin u odnosu na linearne ali nisam siguran u to. Unapred hvala na odgovoru!

http://www.svijetfizike.com/

Odgovor na temu

tomkeus

Član broj: 40478
Poruke: 503
*.eunet.yu.

+6 Profil

Re: Afini prostori???

^{10.07.2008. u 11:58 - pre 218 meseci}

Afini prostori služe da se geometrijska slika o vektorima kao usmerenim dužima dobro definiše (tj. vektori su definisani kao uređeni parovi tačaka). Vektorski prostori su algebarska kategorija i tiču se samo datog skupa i osobina operacija definisanih na njemu bez obzira kakva je realizacija tog skupa, tj. da li su u pitanju strelice, trouglići, babe, žabe itd.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8752
*.dynamic.sbb.rs.

+2807 Profil

Re: Afini prostori???

^{10.07.2008. u 16:14 - pre 218 meseci}

Jedina sustinska razlika izmedju linearnih i afinih prostora je sto u linearnim postoji tacka koja odgovara nula-vektoru (izabrani koordinatni pocetak) a u afinim prostorima su sve tacke potpuno ravnopravne. Od bilo kog linearnog prostora mozes napraviti afini ako "zaboravis" da tacke (to jest vektore) mozes da sabiras, vec da eventualno mozes da ih oduzimas, kada kao rezultat dobijas vektor. Isto tako, od afinog prostora mozes napraviti linearni izborom koordinatnog pocetka.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Afini prostori???

^{10.07.2008. u 18:55 - pre 218 meseci}

U knjizi profesora Musickog ''Matematicke osnove teorijske fizike'' on uvodi pojam prostora kojeg definise kao skup matematickih objekata sa tacno definisanom strukturom. A onda kaze ako je takav prostor snabdeven operacijama sabiranja elemenata prostora i mnozenja istih skalarom onda je to vektorski prostor. Zapravo on pod prostorom smatra afini prostor ili ne kada tako definise?

Citat:

Nedeljko: vec da eventualno mozes da ih oduzimas, kada kao rezultat dobijas vektor

Ne razumem ovo?

Citat:

Nedeljko: Isto tako, od afinog prostora mozes napraviti linearni izborom koordinatnog pocetka.

Kako u afinom da izaberem koordinatni pocetak?

http://www.svijetfizike.com/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8752
*.dynamic.sbb.rs.

+2807 Profil

Re: Afini prostori???

^{11.07.2008. u 08:13 - pre 218 meseci}

Dakle, te objekte (tacke) koje u slucaju vektorskog prostora mozes da sabiras i mnozis skalarom, u slucaju afinog prostora mozes samo da odulzimas, pri cemu je rezultat vektor, pa je

Preciznije govoreci, uvodi se pojam vektora kao klase ekvivalencije uredjenih parova tacaka, ali sa njima mozes da racunas kao da su u pitanju "razlike tacaka".

U afinom prostoru (ako zelis da dobijes vektorski) koordinatni pocetak

biras potpuno proizvoljno, pa onda tacki

pridruzujes vektor

.

Ako bude nejasnoca, onda prepisi definiciju afinog prostora iz knjige ovde, pa da tumacimo sat ostane nejasno.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Afini prostori???

^{17.07.2008. u 20:48 - pre 217 meseci}

Afini

-dimenzioni prostor predstavlja skup tacaka definisanih kao

pri cemu su

koordinate tacke.

Moze li se prihvatiti ovakva def? Cesto se koristi u nekim knjigama iz fizike!

http://www.svijetfizike.com/

Odgovor na temu

R A V E N

Član broj: 36142
Poruke: 1629

+101 Profil

Re: Afini prostori???

^{26.07.2008. u 03:44 - pre 217 meseci}

Npr. baza vektorskog prostora je afina kada vektori koji je sačinjavaju nisu međusobno okomiti i različite su dužine.

Odgovor na temu

Miladinovic
Miladinovic

Član broj: 33748
Poruke: 1892

+44 Profil

Re: Afini prostori???

^{08.02.2009. u 13:22 - pre 210 meseci}

Evo primene i naišao sam na sl. zadatak:
Za ravan definisanu sa x + 2y - 3z =5 odrediti skup rešenja, afini potprostor i direktrisu.

U knjizi G.Kalajdžića ima samo jedan primer, ali mi i dalje nije jasno kako odrediti direktrisu?

Odgovor na temu

Cabo

Član broj: 10942
Poruke: 684
*.rcub.bg.ac.yu.

+5 Profil

Re: Afini prostori???

^{11.02.2009. u 15:02 - pre 210 meseci}

Citat:

Miladinovic: Evo primene i naišao sam na sl. zadatak:
Za ravan definisanu sa x + 2y - 3z =5 odrediti skup rešenja, afini potprostor i direktrisu.

U knjizi G.Kalajdžića ima samo jedan primer, ali mi i dalje nije jasno kako odrediti direktrisu?

Kao sopstveni potprostor generisan sopstvenim vektorima, naravno. Imaš primere sličnih zadataka u „zadacima sa ispitnih rokova“ kod Miše. ;-)

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.dynamic.sbb.rs.

+33 Profil

Re: Afini prostori???

^{17.04.2009. u 12:51 - pre 208 meseci}

Ja bih bio jako srecan kad bi mi ovo bilo tacno?

Gornja transformacija je linearna, a ova ispod nje je afina!

http://www.svijetfizike.com/

Odgovor na temu