Prvo da dodam nešto što sam zaboravio: Sve ono važi samo za stacionarna stanja, a evo sada malo i da razradimo:
Šredingerova jednačina je
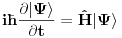
Kada hamiltonijan ne zavisi od vremena, možemo izdvojiti vremensku zavisnost stavljanjem
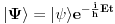
, tako da pošto se vremenske zavisnost skrate, ostane vremenski nezavisna Šredingerova jednačina
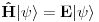
Konkretan oblik hamiltonijana nam sada zavisi od prirode sistema koji razmatramo. Na primer, za naeletkrisanu česticu u električnom polju, hamiltonijan će se sastojati od kinetičke energije i potencijalne energije u električnom polju
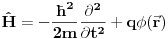
, gde je

električni potencijal (odsad podrazumevamo kordinatnu reprezentaciju). Operatori koji čine hamiltonijan su diferencijalni (kinetička energija) i multiplikativni (potencijal). Svojstvene funkcije ovih operatora su kvadratno integrabilne kompleksne funkcije (eventualno raspodele, ali o tome smo već dovoljno razgovarali ranije). U principu one su iz Lebegovog prstora. Dakle svojstvena stanja su reprezentovana sa
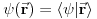
, gde su
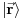
svojstveni vektori operatora položaja. Stacionarna Šredingerova jednačina je sada diferencijalna jednačina
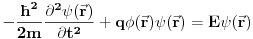
Njoj dualna jednačina
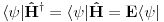
se očigledno dobija običnom kompleksnom konjugacijom, tako da u ovom slučaju važe sledeće jednakosti
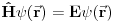
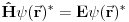
Odavde onda vidimo, da ako neko
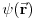
zadovoljava stacionarnu Šredingerovu jednačinu, onda ga zadovoljava i
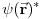
i to za istu svojstvenu vrednost. Kako su oba ova stanja, svojstvena, svojstvena je i njihova linearna kombinacija
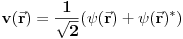
koja je realna. Očekivana vrednost energije u ovom stanju je očigledno ista kao u i polaznim stanjima.
Međutim, šta se dešava kada u igru uđe i magnetno polje? Ako čestica nema spin situacija je relativno jednostavna, jer je klasični hamiltonijan za česticu u EM polju dat sa
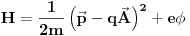
gde su
i

potencijali EM polja. Kada pređemo na kvantnu mehaniku, ove varijable postaju operatori i to opet diferencijalni i multiplikativni pa je situacija ista kao u gornjem slučaju.
Međutim, kada razmatramo čestice sa spinom (a to su sve čestice materije) slika interakcije postaje komplikovanija zato što svaka čestica poseduje sopstveni moment impulsa - spin. Pošto je magnetni moment proporcionalan momentu impulsa imamo da je
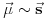
i kako je energija interakcije magnetnog dipola sa spoljašnjim magnetnim poljem
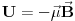
vidimo da će u hamiltonijanu učestvovati i operator spina. Npr. slučaju elektrona imamo da je
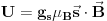
, gde je

žiromagnetni faktor za elektron (oko 2), a
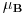
Borov magneton. Pošto spin učestvuje u hamiltonijanu, prostor delovanja hamiltonijana će biti oblika
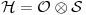
, gde je
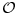
, orbitni prostor stanja, a
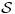
spinski prostor stanja. U orbitnom prostoru stanja deluju operatori koji zavise od konfiguracionih varijabli (položaj, impuls, vreme) tako da je taj prostor Lebegov prostor. Za spinski prostor čestice spina s znamo da je 2s+1-dimenzionalan, tako da će spinski prostor biti reprezentovan odgovarajućim prostorom brojnih kolona. Ovo sada znači da će hamiltonijan biti matrica. Na primer, za spin-pola čestice, hamiltonijan glasi
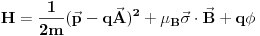
gde je
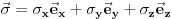
vektor Paulijevih matrica. Dakle, ovaj Hamiltonijan je predstavljen 2x2 matricom. Stanja su oblika
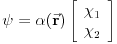
. Ako sada potražimo njima dualna stanja videćemo da su ona oblika
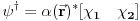
, dakle ona su predstavljena vrstama pa ih ne možemo sabrati. Ovo se generalizuje i za čestice većeg spina. Kod njih je spinski deo prostora predstavljen dužim kolonama i to je jedina razlika.
Dakle, kada nemamo magnetno polje u igri (ili eventualno imamo posla sa česticama bez spina) uvek možemo izabrati bazis tako da stanja budu reprezentovana realnim funkcijama. To je zahvaljujući tom što je prostor dualan prostoru funkcija isti taj prostor funkcija pa nemamo problem sa sabiranjem stanja sa njima dualnim stanjima. Međutim, kada u problemu imamo magnetno polje i spin, nije više moguće sabirati vektore sa njima dualnim vektorima.