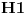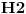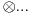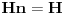Kada imaš sistem od više čestica ukupni prostor stanja je tenzorski proizvod prostora stanja svake čestice i nema tu šta da se vežba, stvar je prosta. Ako imaš dve čestice sa prostorima stanja
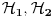
ukupni prostor stanja je
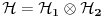
što znači da je ukupno stanje sistema zadato tenzorskim proizvodom elemenata iz svakog prostora, tj. ima formu
.
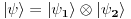
Takođe, ako dinamika jedne čestice dozvoljava razbijanje prostora stanja na faktor prostore primenjuje se isti postupak. Npr. u hamiltonijan za jednu slobodnu 3D česticu je
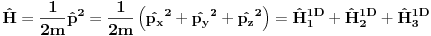
Dakle, hamiltonijan jedne slobodne 3D čestice jednak je sumi hamiltonijana tri slobodne 1D čestice. Ovo onda dozvoljava da se ukupniprostor stanja faktoriše:
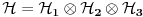
, tj . da ukupno stanje ima formu
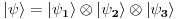
. Stacionarna šredingerova jednačina onda ima formu
\hat{H}|\psi\rangle = \left(\hat{H}_1^{1D}+\hat{H}_2^{1D}+\hat{H}_1^{1D}\right)|\psi_1\rangle \otimes |\psi_2\rangle \otimes |\psi_3\rangle=\left[\left(\hat{H_1^{1D}|\psi_1\rangle\right)\otimes|\psi_2\rangle\otimes|\psi_3\rangle+|\psi_1\rangle\otimes\left(H_2^{1D}|\psi_2\rangle\right)\otimes|\psi_3\rangle+|\psi_1\rangle\otimes|\psi_2\rangle\otimes\left(H_3^{1D}|\psi_3\rangle\right]
Ovo nam onda jedan 3D svojstveni problem prevodi u 3 1D svojstvena problema, pa kada ih rešimo imamo
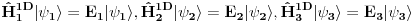
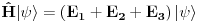
U konkretnom slučaju slobodne čestice znamo da je u koordinatnoj reprezentaciji
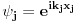
i da je
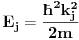
, gde
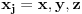
(ovo smo dobili rešavanjem šredingerove jednačine 1D slobodne čestice
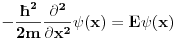
). Tada je ukupna talasna funkcija slobodne 3D čestice
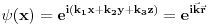
, a energija
.
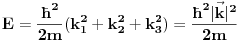
Prosto i linearno.
Neki primer sa vezbi recimo?
