[es] - Kanonske transformacije

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.ns.ac.yu.

+33 Profil

Kanonske transformacije

^{15.11.2007. u 15:57 - pre 212 meseci}

Pitanje je u dokumentu. Unapred hvala na odgovoru!

http://www.svijetfizike.com/

Prikačeni fajlovi

KT.doc - 17k

Odgovor na temu

tomkeus

Član broj: 40478
Poruke: 503
*.eunet.yu.

+6 Profil

Re: Kanonske transformacije

^{17.11.2007. u 00:31 - pre 212 meseci}

1. Kako si dobio onu jednačinu?

2. Generatrisa ne može da zavisi samo od vremena zato što mora da povezuje stare i nove koordinate.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Kanonske transformacije

^{17.11.2007. u 01:02 - pre 212 meseci}

2.)Ja nisam ni rekao da ona mora da zavisi samo od vremena. Nisi pazljivo procitao. Rekao sam da je ona prilicno neodredjena tj. da nije jednoznacno odredjena. Ono sto sam hteo da kazem je sledece

1.)Dobio sam jnu iz Hamiltonovog principa!

http://www.svijetfizike.com/

Odgovor na temu

tomkeus

Član broj: 40478
Poruke: 503
*.eunet.yu.

+6 Profil

Re: Kanonske transformacije

^{17.11.2007. u 03:07 - pre 212 meseci}

Za dati par starih i novih koordinata generatrisa će biti neodređena samo do na aditivnu konstantu, a evo i zašto:

Neka su stare koordinate i impulsi (n koordinata i n njima konjugovanih impulsa)

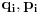
, nove

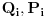
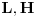
, a odgovarajući lagranžijani i hamiltonijani

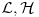
Hamiltonov princip daje

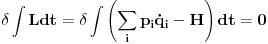
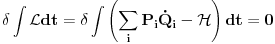
Tj.

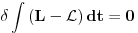
Ovo će uvek biti ispunjeno ako se lagranžijani razlikuju za totalni vremenski izvod neke funkcije F jer

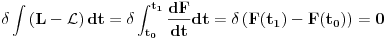
jer je varijacija konstante 0. Ovo nam daje jednačinu

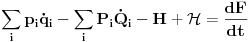
(1)

U opštem slučaju F je funkcija 4n+1 promenljivih

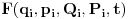
, ali pošto imamo veze starih i novih koordinata

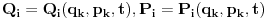
kojih je 2n, sledi da će generatrisa biti funkcija samo 2n+1 promenljivih. Sada imamo četiri varijante za izbor promenljivih od kojih zavisi F

.

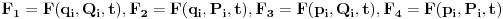
Na primer, u prvom slučaju iz (1) imamo

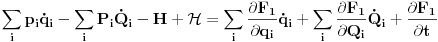
Da bi jednakost važila članovi uz

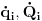
i odgovarajući slobodni članovi moraju biti jednaki što daje

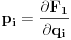
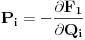
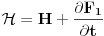
Ako su poznate stare i nove koordinate, kao i hamiltonijani, ovaj sistem diferencijalnih jednačina će odrediti generatrisu do na aditivnu konstantu. U ostala tri slučaja takođe slede slične relacije.

edit: Popravke veze koordinata

_{[Ovu poruku je menjao tomkeus dana 18.11.2007. u 14:06 GMT+1]}

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Kanonske transformacije

^{17.11.2007. u 20:11 - pre 212 meseci}

Samo da napisem kako se dolazi do sledece relacije:

Prikacio sam uz ovu poruku...

Gde je

fja generatrise.

http://www.svijetfizike.com/

Prikačeni fajlovi

1.doc - 25k

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Kanonske transformacije

^{17.11.2007. u 23:23 - pre 212 meseci}

Ako nemas nista protiv ispravio bih jednu gresku u tvojoj poslednjoj poruci!

Trebalo bi da stoji da imamo veze izmedju starih i novih koordinata

, a ne

jer mi je

skup generalisanih koordinata...

http://www.svijetfizike.com/

Odgovor na temu

tomkeus

Član broj: 40478
Poruke: 503
*.eunet.yu.

+6 Profil

Re: Kanonske transformacije

^{18.11.2007. u 14:47 - pre 212 meseci}

Citat:

petarm: Ako nemas nista protiv ispravio bih jednu gresku u tvojoj poslednjoj poruci!

Trebalo bi da stoji da imamo veze izmedju starih i novih koordinata

, a ne

jer mi je

skup generalisanih koordinata...

Popravljeno.

Citat:

petarm: Samo da napisem kako se dolazi do sledece relacije:

Prikacio sam uz ovu poruku...

Gde je

fja generatrise.

Varijacija bilo koje funkcije koja zavisi samo od vremena će uvek biti nula, jer varijacije potiču od menjanja putanja u faznom prostoru. Nisi morao da pišeš sve ono da bi to pokazao, a i btw nešto mi je ono mnogo čudno. Ako sam dobro shvatio ti si donji izraz napisao za pravu faznu trajektoriju sistema i njoj blisku, a potom ih oduzeo.

Ako je to bio slučaj trebalo je da uzmeš u obzir i da će se i hamiltonijan promeniti.

A što se neodređenosti tiče, mislim da sam jasno pokazao da je za date parove koordinata, impulsa i hamiltonijana generatrisa neodređena do na konstantu. Specijalno, ako imaš samo stare i nove koordinate i impulse, ali ne i hamiltonijane, generatrisa će biti neodređena do na funkciju vremena.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.ns.ac.yu.

+33 Profil

Re: Kanonske transformacije

^{19.11.2007. u 12:00 - pre 212 meseci}

Ne vidim zasto bi se Hamiltonova fja menjala u slucaju koji sam napisao?

http://www.svijetfizike.com/

Odgovor na temu

tomkeus

Član broj: 40478
Poruke: 503
*.eunet.yu.

+6 Profil

Re: Kanonske transformacije

^{19.11.2007. u 13:00 - pre 212 meseci}

Variranje putanje

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.ns.ac.yu.

+33 Profil

Re: Kanonske transformacije

^{19.11.2007. u 13:12 - pre 212 meseci}

Ali ja sam oduzeo dva moguca pomeranja pri istoj dinamici!

http://www.svijetfizike.com/

Odgovor na temu

tomkeus

Član broj: 40478
Poruke: 503
*.eunet.yu.

+6 Profil

Re: Kanonske transformacije

^{19.11.2007. u 15:18 - pre 212 meseci}

Nisu sva moguća pomeranja ista. To ti i Hamiltonov princip kaže jer on izdvaja jedno od mogućih pomeranja pri kome je dejstvo minimalno.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.ns.ac.yu.

+33 Profil

Re: Kanonske transformacije

^{21.11.2007. u 10:04 - pre 212 meseci}

Ja sam jednostavno napisao uslov i za druge moguce promene kanonskih promenljivih za isto vreme dt. Ne vidim zasto bi mi se menjale Hamiltonove fje? Mozes li malo detaljnije da obrazlozis svoje misljenje?

http://www.svijetfizike.com/

Odgovor na temu

tomkeus

Član broj: 40478
Poruke: 503
*.eunet.yu.

+6 Profil

Re: Kanonske transformacije

^{21.11.2007. u 12:10 - pre 212 meseci}

Čini mi se da ne razlikuješ invarijantnost forme od totalne invarijantnosti. Evo izraza

Imamo dva seta koordinata. Fiksirajmo sada neku tačku faznog prostora

čime smo automatski zadali vrednosti koordinata

jer prvi i drugi par sebe međusobno jednoznačno određuju. Ovime smo fiksirali i brojne vrednosti članova gornjeg izraza zato što su H,

i F realne funkcije na 6N-dimenzionalnom realnom prostoru. E sada, kada pređemo u neku drugu proizvoljnu tačku i vrednosti ovih funkcija će se promeniti. Međutim, forma ovih funkcija se neće promeniti, tj, formula kojom izračunavaš hamiltonijan je ista u svakoj tački faznog prostora (inače, jelte, reč formula ne bi imala smisla).

Odgovor na temu