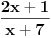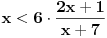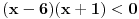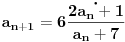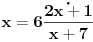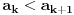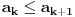Zadat je niz:
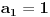
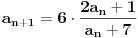
Trebam da dokazem da je konvergentan i nadjem granicnu vrednost.
E sad. Princip monotonije kaze:
Ako je niz monotono rastuci (neopadajuci) i ogranicen sa gornje strane, tada je on konvergentan i tezi svom supremumu.
Ovako, vidi se da niz cine iskljucivo pozitivni racionalni brojevi. Ja sam pretpostavio da vazi:
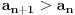
i krenuo da to indukcijom dokazem:
n=1:
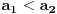
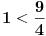
n=k:
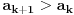 (pretpostavka)
(pretpostavka)k+1:
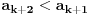
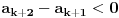
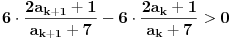
Da se ne bih sada zamarao, kad se ovo malo sredi, svede na zajednicki i svaki sa svakim izmnozi, dobije se ovako nesto:
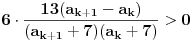
E sad, imenilac je ocigledno uvek pozitivan, jer su svi clanovi niza pozitivni racionalni brojevi, a brojilac
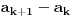 je po pretpostavci uvek pozitivan. Dakle dokazao sam da je tako.
je po pretpostavci uvek pozitivan. Dakle dokazao sam da je tako.E ono sto me ovde muci je sledece: ja sam pretpostavio da je niz rastuci i to sam dokazao. A sta ako je niz npr. neopadajuci? Da se npr. desilo da svaki clan, pored toga sto je veci, moze i biti jednak prethodnom clanu?
Poredici prve clanove ja sam mogao krenuti dokazivati
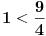 i
i 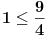 Kako ja mogu prepoznati da li je niz rastuci ili neopadajuci iz ovoga ovde:
Kako ja mogu prepoznati da li je niz rastuci ili neopadajuci iz ovoga ovde: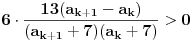
Siguran sam da se tu nekako moze iscitati...




 [ZADATAK] Granicna vrednost rekurentno zadatog niza (ako sam se dobro izrazio)
[ZADATAK] Granicna vrednost rekurentno zadatog niza (ako sam se dobro izrazio)