Dokazaću malo opštije tvrđenje, zbog čega mi i treba ovoliki uvod.
Definicija 1. Neka je

prost broj i
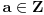
uzajamno prost sa

, onda za

kažemo da je kvadratni ostatak po modulu

akko postoji
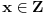
za koje važi
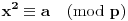
.
Definicija 2. Neka je

prost broj i
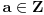
uzajamno prost sa

, onda za

kažemo da je ne-kvadratni ostatak po modulu

akko nije kvadratni ostatak po modulu

.
(ne znam kako bih preveo quadratic non-residue)
Nadalje,

će uvek označavati neki neparan prost broj, a
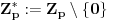
.
Lema 1. Ako je
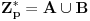
, gde je

skup svih kvadratnih ostataka po modulu

a

skup svih ne-kvadratnih ostataka po modulu

, onda je
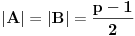
.
Dokaz.
Na osnovu prethodnih definicija jasno je da važi
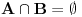
.
Ako je
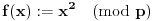
, i ako je
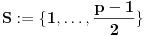
, onda je
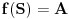
.
Naime,
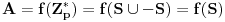
, jer je
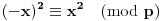
.
Pokazaćemo da je

i injekcija na

.
Ako bi za neke
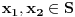
bilo
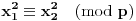
, onda sledi
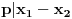
ili
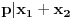
.
Budući da
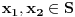
, u prvom slučaju sledi da je
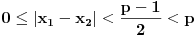
pa mora biti
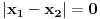
tj.
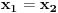
, a drugi je nemoguć zbog procene
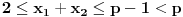
.
Sada imamo da je
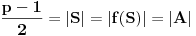
, odakle i sledi tvrđenje.
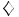 Lema 2.
Lema 2. Ako je
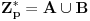
, gde je

skup svih kvadratnih ostataka po modulu

a

skup svih ne-kvadratnih ostataka po modulu

, onda:
1.
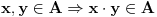
2.

3.
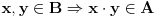
Dokaz.
Primetimo prvo da je, za svako fiksirano
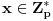
, f-ja
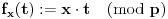
bijekcija na
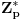
.
Ako je
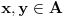
, onda na osnovu definicije 1. sledi da postoje brojevi
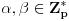
takvi da važi
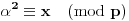
i
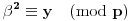
, pa dobijamo
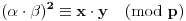
, tj.
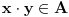
.
Ako je
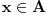
a
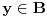
, onda, budući da je

fiksirano, možemo posmatrati f-ju
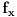
na skupu

. Iz dela pod 1. sledi
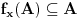
a iz injektivnosti sledi
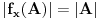
, pa imamo da je
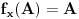
.
Sada je jasno da ne može biti
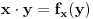
element skupa

, jer bi u protivnom ispalo da za neko

važi
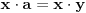
, pa bi, posle skraćivanja sa

ispalo da je
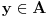
(što je kontradikcija).
Ako je
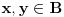
, onda možemo posmatrati f-ju
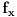
na skupu

, pa koristeći dokazani deo pod 2. kao i injektivnost f-je, na analogan način kao i prethodnom delu, uz korišćnje rezultata
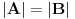
iz Leme 1, dobiti
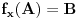
. Sada, na isti način kao i u delu pod 2, sledi da
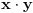
mora biti element skupa

.

(Inače, ove dve leme još lakše slede ako znamo da je za svako prosto p, grupa
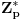
ciklična, ili, što je isto: da za svako prosto

postoji "primitive root modulo

").
Lema 3. Ako je
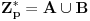
, gde je

skup svih kvadratnih ostataka po modulu

a

skup svih ne-kvadratnih ostataka po modulu

, onda važi:
1. za
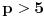
, postoje
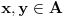
za koje važi
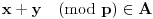
.
2. za
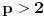
, postoje
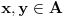
za koje važi
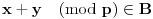
.
Dokaz.
1. Možemo iskoristi identitet:
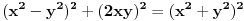
, pazeći pri tom da
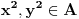
budu takvi da
nije ni
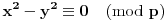
, ni
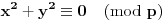
, a to je uvek moguće za
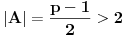
tj. za
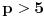
.
2. Budući da je
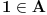
, možemo posmatrati f-ju
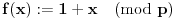
,
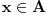
.
Uzmimo da je
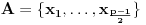
, pri čemu je
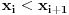
za svako

.
Ako bi za neko

bilo
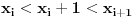
, onda bi moralo biti
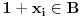
, pa bi to bio kraj dokaza.
A ako bi za svako

bilo
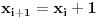
, onda bi imali da je
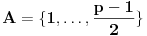
, pa bi moralo biti
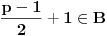
.
 Lema 4.
Lema 4. Svaki element skupa
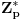
, gde je
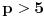
, može se predstaviti kao zbir:
1. Dva kvadratna ostatka, za
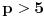
2. Dva ne-kvadratna ostatka, za
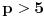
3. Jednog kvadratnog ostatka i jednog ne-kvadratnog ostatka, za
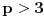
Dokaz:
Ako je
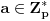
, onda postoji jedinstveno
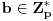
za koje važi
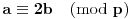
, (jer je 2 inverzibilno po modulu

),
pa ako stavimo da je
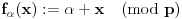
, onda se sve particije broja

u grupi
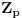
mogu predstaviti kao
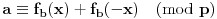
pri čemu se

"šeta" kroz
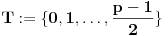
.
Budući da je f-ja
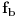
bijekcija i da je
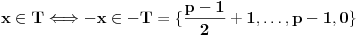
, dobijamo da se svi elementi skupa
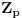
pojavljuju tačno jedanput kao sabirci, u pomenutim razlaganjima, osim što se element

javlja i kao
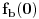
i kao
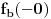
, a što je u stvari jedno te isto. Primetimo i to da su parovi jedinstveno određeni, tj. za dato
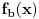
, jedini broj (po modulu p) koji sa njim pravi razlaganje broja

(po modulu p) je upravo
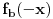
.
Neka su nadalje,

i

skupovi kvadratnih, odnosno ne-kvadratnih ostataka po modulu

.
Neka je
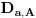
broj razlaganja broja

po modulu

, u kojima su
oba sabirka iz skupa

, (analogan smisao ima i oznaka
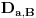
) i neka je
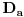
broj "mešovitih" razlaganja broja

po modulu

, u kojima je jedan sabirak iz

a drugi iz

.
Pokazaćemo sada da važi:
a) Ako su
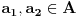
, onda je
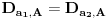
,
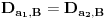
i
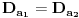
b) Ako su
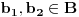
, onda je
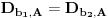
,
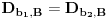
i
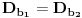
c) Ako je

i
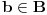
, onda je
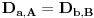
,
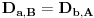
i
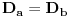
Označimo jedan (bilo koji) od skupova

i

sa

.
Ako su
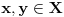
, onda, na osnovu Leme 2. postoji
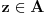
, tako da važi
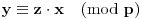
, pa svakom razlaganju broja
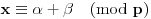
odgovara
jedinstveno razlaganje broja
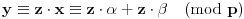
, a pošto je
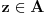
, na osnovu Leme 2. sledi da će i
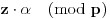
pripadati istom skupu (

ili

) kao i

i analogno,
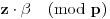
pripadaće istom skupu (

ili

) kao i

. Dakle, vidimo da se "struktura" tih razlaganja ne menja. Pošto možemo napraviti i analogan prelaz sa razlaganja broja

na razlaganja broja

, slede tvrđenja pod a) i b). (Koja u stvari pokušavaju da kažu da prilikom razmatranja broja razlaganja elemenata iz

ili

, nije bitno kog "predstavnika" tih skupova posmatramo.)
Dokaz tvrđenja pod c) je potpuno analogan prethodnom, uz jedinu razliku da
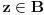
, pa prema Lemi 2, "struktura" razlaganja se "invertuje" tj. ako je
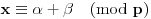
, (neka je npr.
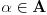
) onda će sabirci u pridruženom razlaganju broja
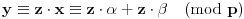
pripadati "suprotnom" skupu (onda je npr.
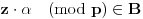
).
Sada, na osnovu Leme 3. i tvrđenja pod a) i b) mora da važi
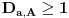
,
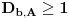
za
svako 
i
svako 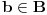
, pa, na osnovu tvrđenja c), dobijamo da je i
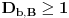
i
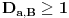
, odakle slede tvrđenja pod 1. i 2.
Da bi važilo i tvrđenje pod 3. dovoljno je pokazati da je za neko
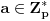
važi
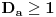
, jer bi na osnovu a), b) i c) odmah sledilo da
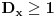
važi i za
svako 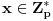
.
Budući da elemenata iz

, odnosno

, ima sasvim dovoljno (za
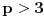
), uvek možemo pronaći

i
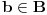
tako da
ne bude
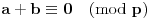
, pa na osnovu prethodne primedbe, važi i tvrđenje pod c).
 Tvrđenje 1.
Tvrđenje 1. Ako je

bilo koji prost broj i

bilo koji ceo broj, onda, ako je
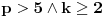
ili
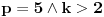
, za svako celo

, uzajamno prosto sa

, postoje celi brojevi

, uzajamno prosti sa

, za koje važi:
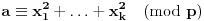
.
Dokaz.
Neka je
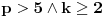
. Dovoljno je dokazati slučaj kada je

, jer se slučaj
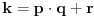
, za
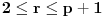
, i
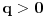
svodi na prethodni tako što uzmemo da
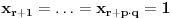
.
Broj

ima
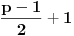
particija u
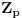
, tj.
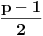
particija u
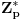
. Izaberimo zato bilo koju particiju,
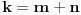
, gde je
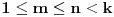
. Sada, za dato celo

, uzajamno prosto sa

, uzmimo da je
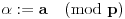
.
Budući da je
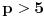
, na osnovu Leme 4, sledi da je
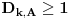
,
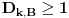
,
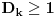
kao i
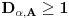
,
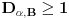
,
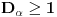
, pa odatle i na osnovu Leme 2, imamo da jednačina
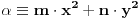
ima rešenja za neke
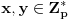
, bez obzira na to kom od skupova

ili

pripadali

i

.
Sada možemo uzeti da je
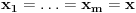
i
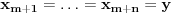
, pa je jasno da mora biti
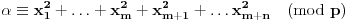
.
Ostao je još slučaj
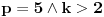
, koji je specifičan po tome što
nije za svako
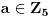
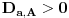
ni
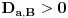
, pa ćemo zato koristiti činjenicu da za
svako 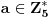
,
jeste 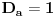
.
Na isti način kao i ranije, vidimo da je dovoljno dokazati tvrđenje u slučaju kad
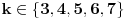
.
Ako
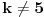
, onda se, zbog
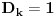
, broj

može razložiti na zbir jednog kvadratnog i jednog ne-kvadratnog ostatka
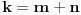
, (3=1+2, 4=1+3, 6=4+2, 7=4+3), pa vidimo da jednačina
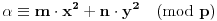
ima rešenja po

i

za svako
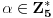
, tako da je, za dato celo
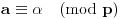
, dovoljno uzeti da je
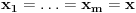
i
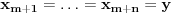
.
Ako je
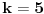
, imamo da je :
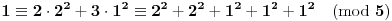
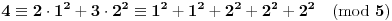
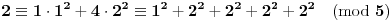
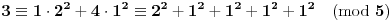 [Ovu poruku je menjao uranium dana 18.08.2005. u 03:50 GMT+1]
[Ovu poruku je menjao uranium dana 18.08.2005. u 03:50 GMT+1]
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.
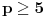 i ceo broj
i ceo broj  ,
, 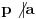 , mogu naći celi brojevi
, mogu naći celi brojevi 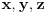 takvi da nijedan od njih nije deljiv sa
takvi da nijedan od njih nije deljiv sa  i da je
i da je 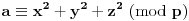 .
.