• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 04.06.2002. Delphi ... 06.02.2003. Projektovanje IS u ERwin-u 24.12.2003. Problem sa relacijama u MSSQL 08.02.2005. Prenos tabela izmedju 2 baze na SQL serveru? 23.09.2005. Kreiranje tabela na SQL serveru iz DataSet-a 12.12.2005. Problem sa relacijama 10.05.2006. Grid sa 15m kabla (gde, iskustva)? 11.09.2006. Skola za SQL i Relaciju MySQL baze 19.12.2006. Pomoć kod MinZaliha 29.07.2010. Mazda 6 ; Honda Accord ili Nissan Altima Navigacija Brisanje liste Aktuelne teme u ovom forumu: Još jedan zadatak sa uglovima Treći zadatak sa uglovima Ostala rešenja algebarske jednačine Lep zadatak sa uglovima Najmanje pozitivno realno r Ikosaedar i gustina ms matematika.... Jedan zadatak sa pravouglim trouglom Japanese | Can you solve this ? | Math.. Jednakostraničan trougao Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Zanimljiv zadatak o uglovima trougla Stado Boga Sunca ... 2000 godina star .. Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

dragan_bg_88 Dragan Slaveski Beograd Član broj: 68739 Poruke: 288 *.dynamic.sbb.co.yu. Profil Problem sa relacijama 05.10.2007. u 10:06 - pre 213 meseci Pozdrav svima. Imam jedan problem, na faxu smo radili relacije ali ne kapiram sledece: Znam sta su relacije, znam i da dokazem koja je relacija poretka i koja je relacija ekvivalencije, ali nisu mi jasen klase ekvivalencije? Sta one zapravo predstavljaju. Znam da postoji neka formula za njih, ali ako neko moze da mi pojasni tu formulu. Isto tako ne razumem sta je to relacija parcijalnog uredjenja? Koliko ja znam klase relacije su ustvari razbijanje relacije na particije, a procitao sam da relacije parcijalnog uredjenja vaze samo za relacije poretka. Meni se cini da razbijanje relacije na particije i relacija parcijalnog uredjenja je jedno isto. Molim vas za pomoc. Hvala... Odgovor na temu

petarm Petar Mali Zrenjanin Član broj: 20220 Poruke: 1879 *.mgnet.co.yu. +33 Profil Re: Problem sa relacijama 05.10.2007. u 12:49 - pre 213 meseci Mislim da je relacija parcijalnog uredjenja isto sto i relacija poretka! http://www.svijetfizike.com/ Odgovor na temu

dragan_bg_88 Dragan Slaveski Beograd Član broj: 68739 Poruke: 288 *.dynamic.sbb.co.yu. Profil Re: Problem sa relacijama 05.10.2007. u 22:10 - pre 213 meseci A jel moze neko to malo da mi pojasni? Odgovor na temu

qdot Mladen Srdic Nova Pazova Član broj: 51019 Poruke: 25 217.169.219.* Profil Re: Problem sa relacijama 05.10.2007. u 23:08 - pre 213 meseci Ako se ja dobro secam, klasa ekvivalencije za odredjeni elemenat skupa X (oznachimo ga sam malim x) je skup svih onih elemenata skupa X koji su u relaciji sa x, ukljuchujuci i taj elemenat (jer je relacija simetrichna). Dakle , gde sam sa oznachio relaciju. Odgovor na temu

Farenhajt Goran Kapetanović Beograd Član broj: 78132 Poruke: 449 *.tehnicom.net. +6 Profil Re: Problem sa relacijama 05.10.2007. u 23:22 - pre 213 meseci Evo na primeru: Recimo da je na skupu data relacija ekvivalencije "imaju isti ostatak pri deljenju za 7" (ostavljam tebi da dokažeš da to zaista jeste relacija ekvivalencije). 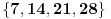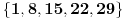Klase ekvivalencije sad su naprosto podskupovi s odgovarajućim "nadnaslovom": Klasa "imaju ostatak nula": Klasa "imaju ostatak jedan": Klasa "imaju ostatak dva": . . . 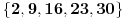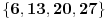Klasa "imaju ostatak šest": Unutar svake klase svaki je element sa svakim u relaciji, a elementi iz različitih klasa međusobno nisu u relaciji. Figurativno rečeno, klase ekvivalencije pokazuju ko je tu kome "rodbina", a ko nije. Odgovor na temu

dragan_bg_88 Dragan Slaveski Beograd Član broj: 68739 Poruke: 288 *.dynamic.sbb.co.yu. Profil Re: Problem sa relacijama 06.10.2007. u 12:07 - pre 213 meseci Razumeo sam klase ekvivalencije, hvala vam na odgovoru. A da li bi jos neko mogao da mi pojasni relaciju parcijalnog uredjenja? I jos jedna stvar, kod relacija parcijalnog uredjenja spominju se maximalni lanci, ako moze objasnjenje i za to... Odgovor na temu