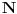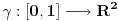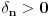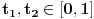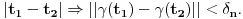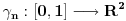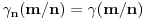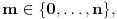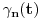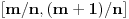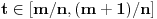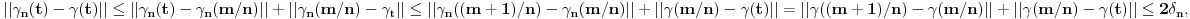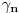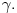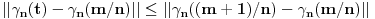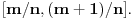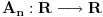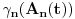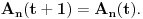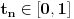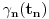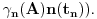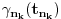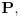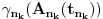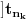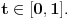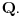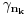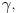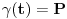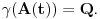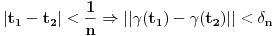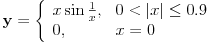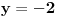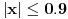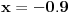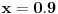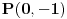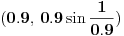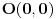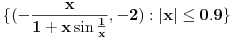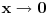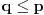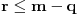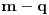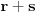Re: Zanimljivi zadaciCitat:
Prihvatio bih, naravno (nikad ne uplićem filozofske stavove u rešavanje matematičkih problema).
Citat:
uranium:
a ako prihvataš, e onda bih voleo da mi objasniš u čemu je suštinska razlika između te i one prethodne situacije sa krivom
a ako prihvataš, e onda bih voleo da mi objasniš u čemu je suštinska razlika između te i one prethodne situacije sa krivom
Manja razlika je u tome što tvoja funkcija za jedan broj izbaci jednu vrednost bez ikakvih problema, dok u našem slučaju moramo pratiti šta se dešavalo od samog početka. Veća razlika je u tome što jesam prihvatio da je funkcija definisana na celo
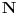, ali nije definisana u tački 
. Kao što možeš da zaređaš po prirodnim brojevima i do svakog konkretnog bi stigao pre ili kasnije, tako možeš da zaređaš i po onim bregovima i svaki konkretan bi došao na red pre ili kasnije, ali ne i koordinatni početak (koji je „iza“ svih njih, kao što je „iza“ svih prirodnih brojeva).Da rekapituliramo stvari. Prvo smo imali konveksne krive i postupak za njih (vrtimo jednu tačku, drugu uzimamo u jedinstveno preseku). Onda smo unapredili postupak tako da prelazi i ispupčenja; jasno je, ako pređe jedno, onda može i konačno mnogo. E sad bi trebalo još da unapredimo da prolazi beskonačno mnogo ispupčenja. Ti tvrdiš da možemo uzeti limes i da će sve biti OK, a meni to jednostavno nije dovoljno čisto: najpre uopšteno, a zatim i na osnovu čega tvrdiš da ćemo time zaobići i sve patološke slučaje (recimo, ni na osnovu čega ne možemo tvrditi da po
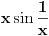idemo pravo prema nuli; ako se nešto „dešava“ s druge strane, onda ćemo morati i po ovim talasićima da idemo napred-nazad, a ne samo da ih pratimo do nule). Štaviše, možemo primetiti da se prelaz između prve situacije (konveksne krive) i druge zasnovao na obradi „specijalnih“ tačaka (onih na vrhu „brega“ i na dnu „doline“), te smo rekli šta treba raditi kad dođemo do njih. Moraćeš se složiti da u trećem scenariju imamo jednu još „specijalniju“ tačku (nulu), jer se ona ne uklapa u tačke s kojima smo do sada radili, pa očekujem da će krpljenje tog slučaja uključivati i neko uputstvo u vezi s tom tačkom. Reći da limes pušten kroz drugi slučaj pokriva sve odjednom suviše mi je klimavo.I za kraj, vrlo sličan argument upotrebljen je u tekstu koji sam okačio (mi ovde rotiramo pravu oko tačke
, tamo je transliramo gore-dole), a ovo mu je pronađeno kao jedan od propusta. Procenio sam (mada, naravno, uvek postoji šansa da grešim) da je ovo i najteže prevazići; dakle, ako uspeš da ubediš matematičku zajednicu kako se taj slučaj pokriva jednostavnom nadgradnjom prethodnog, eto ti šanse da rešiš problem star stotinak godina. Ljubičice crvena, što si plava kô zelena trava.
]: zbog jedinstvenosti "rešenja" svake doline/brega imamo validan algoritam za svaki, a time i za sve doline/bregove. Oni se moraju neprekidno preslikati na drugi kraj krive a zbog neprekidnosti same krive, i tačka singulariteta nema gde da pobegne...
