Citat:
pravim_se_tosa: Burcham i Marinkov --koriscene knjige. (takodje William R. Leo)
Meni ovo "tako je po definiciji" ne pije bas vodu a drugo je "posledica" prvog (po meni je to isti tip odgovora kao sto napisah:"eksperiment je pokazao da ne mogu 2 e u isto stanje pa su stimali teoriju, pa su posle otkrili cestice za koje to ne vazi pa su ih nazvali bozonima").
Ja ta dva podatka znam ali kazem nije mi jasno. Dosta mi je da u knjigama pise "ova je nuzno antisimetricna". Stanja koje opisuje antisimetricna funkcija je za energiju izmene 2K stabilnije od stanja koje opisuje simetricna, pa pomislih da tu lezi zec.Kazem dosta mi je da pamtim (malte ne napamet) da ukoliko je spinska funkcija simetricna mora biti da je prostorna antisimetricna. Jednostavno me nerviraju takve stvari pa rekoh da okacim da li neko ima lepse objasnjenje.
Vidim da mešaš (barem iz tvog pisanja mi se tako čini) simetričnost u prostornom smislu (parnost) sa simetričnošću u odnosu na izmene čestica. Klasifikacija na bozone i fermione potiče iz ovog potonjeg.
Postulat nerazlikovanja čestica nam kaže da ako u npr. dvočestičnom sistemu razmenimo čestice ukupno stanje ne sme da se promeni. U sistemu od dve čestice permutaciona grupa se svodi na jedinični element i transpoziciju. Ako je operator transpozicije čestica označen sa
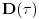
, a stanje sistema je
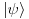
na osnovu postulata o nerazličivosti imamo
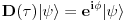
pošto su sva stanja fizički ekvivalentna do na fazni faktor. Dvostruka primena transpozicije vraća sistem u početno stanje, tj.
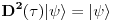
što rezultira time da mora da važi
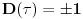
. Dakle transpozicija čestica ili menja znak stanja ili ga ostavlja nepromenjenim. Sva stanja koja menjaju znak pri transpoziciji čine antisimetrični potprostor, a ona koja ne menjaju znak čine simetrični potprostor. Recimo sada da je neka čestica u stanju koje se delom sastoji od simetričnog
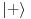
i delom antisimetričnog
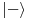
, tj.
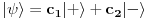
. Ako sada na njega delujemo operatorom transpozicije imamo
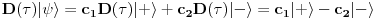
što više nije kolinearno sa početnim stanjem pa ne predstavlja više fizički identično stanje što znači da je postulat o nerazličivosti narušen. Stoga su čestice ili u isključivo simetričnim ili u isključivo antisimetričnim stanjima. Ovo nam onda nameće kategorizaciju čestica po potprostoru u kome leže njihova stanja. Čestice opisane vektorima iz simetričnog potrpostora zovemo bozonima, a čestice opisane vektorima iz antisimetričnog dela zovemo fermionima.
U prethodnoj poruci sam pokazao kako iz svojstva antisimetričnosti sledi Paulijev princip isključenja. Iz ovoga onda imamo da, ako se neki sistem može naći u prebrojivom skupu stanja, će brojevi popunjenosti stanja za fermione biti 0,1,a za bozone 0,1,2,... Ovo nam onda daje Boze-Ajnštajnovu i Fermi-Dirakovu statistiku.
Što se dela sa spinom tiče, jednoznačnu vezu nam daje Paulijev teorem i stoga nam je potpuno svejedno da li su bozoni i fermioni definisani na osnovu spina ili simetričnosti na dejstvo permutacione grupe.
Stoga, ako je kompozitna čestica sastavljena od bozona ili parnog broja fermiona, ona će biti bozon pa njeno totalno stanje mora biti simetrično u odnosu na izmenu čestica. Ukoliko je kompozitna čestica sastavljena od neparnog broja fermiona, ona će biti fermion pa je njeno totalno stanje antisimetrično. Ove stvari nam onda služe za konstrukciju ukupnog stanja kompozitnog sistema.
Evo primera. Imamo od sistem dve čestice a i b spina
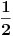
sa bazisom u orbitnom prostoru stanja (tj. prostorni delovi stanja)
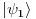
i
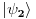
. Sistem sastavljen od ove dve čestice ima spin 1 pa je bozon. Sabiranjem spinova dolazimo do bazisa u ukupnom spinskom prostoru
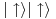
,
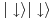
,
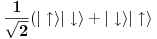
i
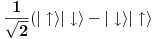
. Prve tri spinska stanja su simetrična što znači da i prostorni deo mora biti simetričan tako da će on biti
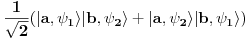
. Četvrto spinsko stanje je antisimetrično što znači da i prostorno stanje mora biti antisimetrično pa će ono biti
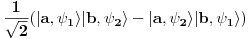
. Na taj način dobijamo ukupna stanja sistema (ovde obrati pažnju da smo zanemarili efekat interakcije čestica koji bi doveo do toga da jednočestični bazis nije dobra osnova za formiranje dvočestičnog bazisa). Ako je hamiltonijan sistema
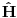
očekivana vrednost energije u stanju
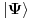
koje može biti bilo koje od prethodnih stanja je
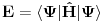
. Ako spinovi ne interaguju onda njih možemo izostaviti i možemo izmnožiti samo prostorne delove stanja. Prostorni delovi stanja imaju formu
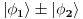
. Kada ovo stavimo u izraz za očekivanu vrednost i iskoristimo identičnost čestica (
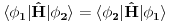
) dobijamo
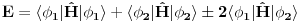
. Znak plus odgovara simetričnom prostornom stanju, a znak minus antisimetričnom. Ako je hamiltonijan pozitivni operator (tj. svojstvene vrednosti su mu veće nule) što je čest slučaj kod slabointeragujućih sistema vidimo da će antisimetrično prostorno stanje imati manju energiju što znači da je stabilnije. Nadam se da ovo odgovara na drugi deo tvoje poruke.
[Ovu poruku je menjao tomkeus dana 16.07.2007. u 14:31 GMT+1]