Srodne teme

31.05.2002. integral
18.01.2003. MouseEventArgs delta
28.08.2004. Mastercard - POS terminali Delta banke
20.11.2004. Delta banka online..... Kako placati racune?
05.03.2005. Prodata Delta banka - 75% kapitala za 277.500.000..
14.03.2005. Povezanost količine gibanja i impulsa sile
08.12.2005. Nema vise Delta banke
22.01.2006. Delta life osiguranje
26.01.2010. Yakumo delta 300 GPS

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.

Dirakova delta f-ja

[es] :: Fizika :: Dirakova delta f-ja

Strane: 1 2

[ Pregleda: 12796 | Odgovora: 24 ] > FB > Twit

Autor

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
212.200.54.*

+33 Profil

Dirakova delta f-ja

^{14.04.2007. u 23:01 - pre 219 meseci}

Voleo bih da mi neko objasni zasto je izvod Hevisajdove f-je delta f-ja i koji je njen znacaj.

http://www.svijetfizike.com/

Prikačeni fajlovi

Delta fja.doc

Delta fja.doc - 19k

Odgovor na temu

mcetina2
Marko Cetina
Grad student (fizika)
Cambridge, MA (SAD)

Član broj: 125398
Poruke: 220
*.MIT.EDU.

Profil

Re: Dirakova delta f-ja

^{15.04.2007. u 00:02 - pre 219 meseci}

Hint:

nije funkcija. Medjutim,

jeste dobro definisan linearni operator za dovoljno glatke funkcije f(x). Ako hoces da budes matematicki precizan, treba pricati o ovom operatoru a ne o samoj delta-"funkciji".

Stvari poput delta "funkcije" koje smisla imaju samo pod znakom integrala u analizi su poznate kao distribucije. Veoma su korisne za opis diskontinuiteta, singulariteta i tako toga....

Odgovor na temu

Milan Milosevic

Član broj: 67
Poruke: 932
91.150.121.*

+31 Profil

Re: Dirakova delta f-ja

^{15.04.2007. u 06:58 - pre 219 meseci}

Kad funkcija trpi konacan skok u nekoj tacki tad njen prvi izvod trpi beskonacan skok.
To se moze objasniti najprostije preko same definicije izvoda H'(x)=dH(x)/dx.
Ovde mozemo dx=x2-x1 posto ovde dx tezi nuli, a 1/0 tezi beskonacno, te je odavde i
H'(0)=beskonacno, a u ostalom delu prostora po definiciji izvoda iz konstante nula.
To i jeste definicije dirakove delta funkcije.

Odgovor na temu

Fitopatolog
Dušan Marjanov
Novi Sad

Član broj: 90936
Poruke: 683
91.150.98.*

+3 Profil

Re: Dirakova delta f-ja

^{15.04.2007. u 21:54 - pre 219 meseci}

Delta f-ja spada u generalisane (tzv nesvojstvene) f-je koje nisu f-je u pravom smislu (reč je o familiji f-ja) zato što:
može imati bilo koju vrednost u intervalu (-w,w), gde w->0,
van tog intervala vrednost je nula,
a inetgral (površina ispod krive) u tom intervalu mora biti 1.

Hevisajdova f-ja pripada istoj kategoriji f-ja, pri čemu je:
vrednost f-je jednaka 0 od -beskonačno do -w
od -w do w vrednost nije strogo definisana (w->0), ali vazi H(x)=integral od -w do x (D(t) dt)
vrednost f-je je 1 posle w

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.ns.ac.yu.

+33 Profil

Re: Dirakova delta f-ja

^{18.04.2007. u 08:13 - pre 219 meseci}

A zasto je kod Hevisajdove f-je vrednost u 0 bas 1/2? I da li tako to tretiraju i matematicari ili oni Hevisajdovoj f-ji daju recimo vrednost 0 u 0?

http://www.svijetfizike.com/

Odgovor na temu

Fitopatolog
Dušan Marjanov
Novi Sad

Član broj: 90936
Poruke: 683
77.46.183.*

+3 Profil

Re: Dirakova delta f-ja

^{18.04.2007. u 22:15 - pre 219 meseci}

To je anomalija Laplasove (Furijeove?) transformacije. Napravi Furijeovu transformaciju f-je H(t) pa potraži inverznu - u tom slučaju će ti se pojaviti da je Hinv(0)=1/2. Po definiciji H(t) za t=0 nije striktno ograničeno na 1/2, važi definicija iz mog prethodnog posta.

pogledaj
http://mathworld.wolfram.com/HeavisideStepFunction.html
deo pri dnu strane koji se odnosi na Furijeovu transformaciju Hevisajdove f-je. Uz Delta-funkciju je član 1/2, koji će pri inverznoj transformaciji dati vrednost 1/2 u nuli.

_{[Ovu poruku je menjao Fitopatolog dana 18.04.2007. u 23:26 GMT+1]}

Odgovor na temu

Fitopatolog
Dušan Marjanov
Novi Sad

Član broj: 90936
Poruke: 683
77.46.229.*

+3 Profil

Re: Dirakova delta f-ja

^{19.04.2007. u 22:07 - pre 219 meseci}

Evo i nešto preciznijeg odgovora:
Pošto H(t) (Hevisajdova ili odskočna f-ja) ne zadovoljava Dirihleov uslov ne može da ima Furijeovu transformaciju, bar ne u nekom "normalnom" obliku. Da bi se ipak došlo do Furijeove transformacije H(t) pribegava se triku: Traži se Furijeova transformacija f-je h(t)=H(t)-H(t-T), što je u stvari impuls širine T. h(t) ima Furijeovu transformaciju:
F(h(t))=(1-exp(-j*w*T))/(j*w)
a ako se pusti da T teži beskonačnosti impuls se pretvara u Hevisajdovu f-ju, pa se dobija sledeći izraz za Furijeovu transformaciju:
H(w)=pi*D(w) + 1/(j*w)
D je Dirakova f-ja.
Inverzna Furijeova transformacija od H(w) će ponovo dati vrednost h(t), ali će član pi*D(w) dati vrednost 1/2 za t=0.

Literatura: Ilija Stojanović: Osnovi Telekomunikacija, Građevinska knjiga 1977, strana 190-192

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.ns.ac.yu.

+33 Profil

Re: Dirakova delta f-ja

^{25.04.2007. u 08:54 - pre 219 meseci}

Ja sam cuo od jednog profesora da se to 1/2 uvodi zbog Fermi - Dirakove statistike.

http://www.svijetfizike.com/

Odgovor na temu

Fitopatolog
Dušan Marjanov
Novi Sad

Član broj: 90936
Poruke: 683
77.46.230.*

+3 Profil

Re: Dirakova delta f-ja

^{25.04.2007. u 19:58 - pre 219 meseci}

Kakve tegobe ima rečena statistika ako se ne uvede ova 1/2?

Odgovor na temu

Fitopatolog
Dušan Marjanov
Novi Sad

Član broj: 90936
Poruke: 683
77.46.177.*

+3 Profil

Re: Dirakova delta f-ja

^{30.04.2007. u 20:14 - pre 219 meseci}

Takođe je interesantan i Gibsov fenomen, videti:

http://mathworld.wolfram.com/GibbsPhenomenon.html

http://en.wikipedia.org/wiki/Gibbs_phenomenon

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.ns.ac.yu.

+33 Profil

Re: Dirakova delta f-ja

^{15.05.2007. u 09:48 - pre 218 meseci}

Ne znam to bih i ja voleo da znam. Verovatno nije zbog teskoca nego zbog bolje fizicke interpretacije.

http://www.svijetfizike.com/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.sr.gov.yu.

+2801 Profil

Re: Dirakova delta f-ja

^{15.05.2007. u 16:25 - pre 218 meseci}

Citat:

mcetina2: Hint:

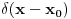
nije funkcija. Medjutim,

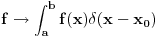
jeste dobro definisan linearni operator za dovoljno glatke funkcije f(x).

Nije mi baš najjasnije kako može biti dobro definisan integral nečega što nije dobro definisano. No, pustimo sad to.

Sa

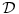
označimo skup svih beskonačno diferencijabilnih funkcija

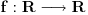
takvih da je skup

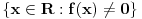
ograničen. Elemente skupa

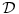
zovemo osnovnim funkcijama.

Za proizvoljne realne funkcije

definisane na istom domenu

i proizvoljne realne konstante

pod funkcijom

podrazumevaćemo funkciju

definisanu jednakošću

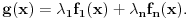
U tom slučaju, funkciju

zovemo i jednom linhearnom kombinacijom funkcija

Skup

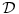
obrazuje vektorski prostor, što znači da je linearna kombinacija funkcija iz tog skupa takođe u tom skupu. Pod linearnim funkcionalom podrazumevaćemo preslikavanje

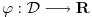
za koje je

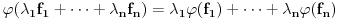
za ma koje

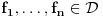
i

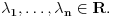
Za niz funkcija

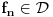
ćemo reći da konvergira ka funkciji

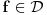
kada

teži beskonačnosti i pisaćemo

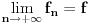
ako postoji ograničen skup

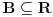
takav da je

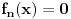
za svako

i

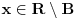
i ako za svaki prirodan broj

i svako

postoji prirodan broj

takav da za svako

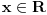
i svako

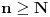
važi

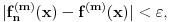
gde

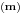
označava

-ti izvod date funkcije.

Za niz realnih brojeva

ćemo reći da konvergira ka realnom broju

kada

teži beskonačnosti i pisaćemo

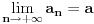
ako za svako

postoji prirodan broj

takav da za svako

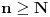
važi

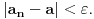
Pod distribucijom podrazumevamo liearni funkcional

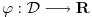
takav da za ma koje

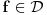
i niz

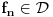
za koji je

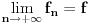
važi

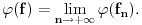
Skup svih distribucija obeležavamo sa

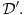
Ako je

distribucija, a

osnovna funkcija, umesto

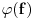
pisaćemo

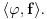
Preslikavanje koje svakoj osnovnoj funkciji pridružuje njenu vrednost u tački 0 ispunujava uslove iz definicije distribucije. Obeležavamo ga sa

i zovemo je Dirakovom distribucijom. Dakle, po definiciji Dirakove distribucije je

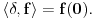
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.sr.gov.yu.

+2801 Profil

Re: Dirakova delta f-ja

^{15.05.2007. u 16:47 - pre 218 meseci}

Ako je

lokalno integrabilna funkcija (što znači da na svakom ograničenom intervalu ima smisla govoriti o njenom integralu), onda se odgovarajuća distribucija obeležava istim simbolom i definiše sa

To je uvek distribucija i distribucije koje opisanim postupkom nastaju od obi;nih lokalno integrabilnih funkcija yovemo regularnim ditribucijama. Sve ostale distribucije zovemo singularnim. Dirakova distribucija je primer singularne distribucije. Sa druge strane, izvod

proizvoljne distribucije

(regularne ili singularne) se definiše jednakošću

Najzad, da izračunamo izvod Hevisajdove distibucije H. Za proizvoljno

važi

Pošto ovo važi za svako

sledi da je

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
82.208.193.*

+33 Profil

Re: Dirakova delta f-ja

^{20.05.2007. u 16:37 - pre 218 meseci}

Mislim da je ovo i istorijski veoma zanimljivo. Naime Dirak je napisao "Metode kvantne fizike" gde je pomocu delta fje uradio sva izvodjenja i dobio rezultate. Kasnije je Neumann sve ovo egzaktno izveo matematicki primenom mera i to napisao u delu "Matematicke metode kvantne fizike", ali je dobio rezultate koji su se poklapali sa Dirakovim :) Te nije oborio Dirakovu teoriju vec joj je samo pomogao da stane na noge!

http://www.svijetfizike.com/

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Dirakova delta f-ja

^{15.07.2007. u 20:00 - pre 216 meseci}

Imam pitanja. Naime receno je gore da je delta fja linearan operator, ali takodje i da je distribucija. Da li je pravilno reci da je nesto i operator i distribucija? To me malo zbunjuje. I da li je pravilno reci da je delta fja prosirenje Kronekerovog delta simbola na kontinuum? Zaista bih voleo da neko odgovori na ova pitanja! I zaista me buni kad neko kaze "dovoljno" glatka fja ili "dovoljno" lepa fja ili sl

Sta znaci to "dovoljno" i koliko je to "dovoljno"? Unapred hvala na odgovoru!

http://www.svijetfizike.com/

Odgovor na temu

tomkeus

Član broj: 40478
Poruke: 503
*.eunet.yu.

+6 Profil

Re: Dirakova delta f-ja

^{16.07.2007. u 00:55 - pre 216 meseci}

Citat:

petarm: Imam pitanja. Naime receno je gore da je delta fja linearan operator, ali takodje i da je distribucija. Da li je pravilno reci da je nesto i operator i distribucija? To me malo zbunjuje. I da li je pravilno reci da je delta fja prosirenje Kronekerovog delta simbola na kontinuum? Zaista bih voleo da neko odgovori na ova pitanja! I zaista me buni kad neko kaze "dovoljno" glatka fja ili "dovoljno" lepa fja ili sl :) Sta znaci to "dovoljno" i koliko je to "dovoljno"? Unapred hvala na odgovoru!

Ja se nadam da ovde nisu pomešao pojam distribucije u statističkom smislu i pojam distrubucije u funkcionalnoj analizi. Delta funkcija je ovo drugo. Inače u prostor distribucija

u funkcionalnoj analizi se definiše kao skup linearnih funkcionala (odatle operatorski deo) koji deluju na prostor

, tj. prostor svih beskonačno diferencijabilnih funkcija koje su van nekog konačnog intervala jednake nuli. Dakle distribucija

je preslikavanje

koje je pri tome linearno tj. za

i

važi

gde su a i b konstante . Pri tome su distribucije neprekidne u odnosu na Švarcovu konvergenciju u

, tj za niz funkcija

koji konvegira u Švarcovom smislu ka funkciji

važi da

(ovo je ono što je Nedeljko napisao samo na malo fizičarskiji način).

Prostor svih beskonačno diferencijabilnih funkcija koje su van nekog konačnog intervala jednake nuli je uzet upravo zbog svojstva "dovoljne glatkosti". Matematičarima to nije bitno i njima su daleko interesantniji funkcionalni prostori koji nisu tako "pitomi". Međutim, pošto je analiza osnovno matematičko oruđe kojim se služe fizičari, njima je potrebno da funkcije uvek mogu da se diferenciraju, integrale, razvijaju u redove itd. do mile volje. Srećna okolnost (možda je ovde bolje upotrebiti reč "nužnost") je da se priroda zapravo i ponaša na "gladak" način, tj. malom uzroku odgovaraju i male posledice (u malim vremenskim intervalima) tako da su u osnovi funkcije kojima opisujemo prirodu glatke. Usput je ubačen i zahtev da funkcije budu nenulte samo unutar nekog konačnog intervala što odgovara prirodi jer su u osnovi svi sistemi kojima se bavimo lokalizovani u konačnom delu prostora (ma koliko veliki on bio)

_{[Ovu poruku je menjao tomkeus dana 16.07.2007. u 10:46 GMT+1]}

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.mgnet.co.yu.

+33 Profil

Re: Dirakova delta f-ja

^{16.07.2007. u 01:57 - pre 216 meseci}

Ja bih ustvari distribucije u smislu funkcionalne analize mogao definisati kao granice neprekidnih fja. Zar ne?

http://www.svijetfizike.com/

Odgovor na temu

tomkeus

Član broj: 40478
Poruke: 503
*.eunet.yu.

+6 Profil

Re: Dirakova delta f-ja

^{16.07.2007. u 10:49 - pre 216 meseci}

Da. Dokazuje se da se prostor raspodela

sastoji od limesa Koši-konvergentih nizova iz

Odgovor na temu

tomkeus

Član broj: 40478
Poruke: 503
*.eunet.yu.

+6 Profil

Re: Dirakova delta f-ja

^{16.07.2007. u 13:47 - pre 216 meseci}

Citat:

petarm: I da li je pravilno reci da je delta fja prosirenje Kronekerovog delta simbola na kontinuum?

U rigoroznom matematičkom smislu: Nemam pojma, zato što ne znam kako matematičari definišu "proširenje" Kronekereovog simbola na kontinuum, ako uopšte to i rade.

U smislu analogija: Može se reći zato što ako integral posmatramo kao "kontinualnu sumu" delta funkcija se ponaša kao Kronekerov simbol zato što "ubija" sumu. Slikovitije:

Ovako deluje Kronekerov simbol

Ovako deluje delta funkcija

Kao što vidiš, upotreba je totalno analogna.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
82.208.193.*

+33 Profil

Re: Dirakova delta f-ja

^{16.07.2007. u 21:16 - pre 216 meseci}

Znam to. Dirakova delta fja i ima to delta u imenu od Kronekerovog delta simbola. Iz razloga koji si naveo. Pitanje ostaje i dalje da li delta fju mogu posmatrati kao prosirenje Kronekerovog delta simbola na kontinuum?

http://www.svijetfizike.com/

Odgovor na temu

[es] :: Fizika :: Dirakova delta f-ja

Strane: 1 2

[ Pregleda: 12796 | Odgovora: 24 ] > FB > Twit

Srodne teme

31.05.2002. integral
18.01.2003. MouseEventArgs delta
28.08.2004. Mastercard - POS terminali Delta banke
20.11.2004. Delta banka online..... Kako placati racune?
05.03.2005. Prodata Delta banka - 75% kapitala za 277.500.000..
14.03.2005. Povezanost količine gibanja i impulsa sile
08.12.2005. Nema vise Delta banke
22.01.2006. Delta life osiguranje
26.01.2010. Yakumo delta 300 GPS

Navigacija

Lista poslednjih: 16, 32, 64, 128 poruka.