Srodne teme

26.06.2004. Moram uzeti neki olympus do 600 KM (300Eura), koj..
18.07.2004. 1.PC WIN XP sa PRINTEROM HP 1100 2.PC WIN NT. Št..
04.02.2005. Veliki broj provera dužine pesama
28.04.2005. Legenda o Hanojskim kulama
04.05.2005. WinXP na 300 MHz
20.12.2010. Elektronski regulator temperature do 300 stepeni
28.10.2005. Spajanje kabelske televizije u zgradi
09.04.2006. Golf 2 1.6 TD Neravnomeran rad motora
05.10.2006. Epson LX-300+ problem sa logickom plocom
12.11.2009. Dimenzije pločice za UNIVERSAL P-300

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.

Misaoni eksperiment - štap dužine 300,000km

[es] :: Fizika :: Misaoni eksperiment - štap dužine 300,000km

Strane: 1 2

[ Pregleda: 5623 | Odgovora: 22 ] > FB > Twit

Autor

Daniel011
Beograd

Član broj: 76088
Poruke: 1101
*.dynamic.sbb.co.yu.

ICQ: 2336441

+3 Profil

Misaoni eksperiment - štap dužine 300,000km

^{19.04.2007. u 14:22 - pre 219 meseci}

Ovaj problem mi je pao na pamet još pre 15 godina, tražio sam odgovor kod raznih ljudi (među kojima je bilo i profesora fizike), ali ne samo da su odgovori bili prilično različiti, nego nisu bili ni dovoljno uverljivi. Radi se o sledećem:

Pretpostavimo da je na raspolaganju idealno krut štap dužine 300,000km (dakle, dužina koju svetlost pređe za jednu sekundu). Na jednom kraju štapa se nalazim ja, a na drugom kraju štapa moj pomoćnik. U trenutku t=0 ja gurnem štap za neki određeni pomeraj. Ono što me interesuje je, da li će se štap na pomoćnikovom kraju pomeriti u istom trenutku kada sam ja štap gurnuo, ili će se pomeriti jednu sekundu kasnije?

I onda potpitanje za bilo koji od ova dva slučaja:

1) u slučaju da će se štap na drugom kraju pomeriti istovremeno kad i na prvom, pošto pomeranje štapa možemo shvatiti kao prenošenje nekih informacija (slično Morzeovoj azbuci), dolazimo do zaključka da je informaciju moguće slati ne brzinom svetlosti nego trenutno, tj. beskonačnom brzinom??

2) u slučaju da će se štap na drugom kraju pomeriti jednu sekundu posle njegovog pomeranja na prvom kraju, šta se u toku te jedne sekunde događa sa dužinom štapa, s obzirom da je on idealno krut, tj. nije podložan istezanju niti sabijanju?

Odgovor na temu

Not now, John!

Član broj: 231
Poruke: 1318
87.250.121.*

+4 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{19.04.2007. u 15:13 - pre 219 meseci}

Pošto ne postoji apsolutno krut štap, onda i ne možeš ništa korisno zaključiti iz tog misaonog eksperimenta. Potrebno ti je da znaš kojom brzinom se prostiru zvučni talasi kroz takav štap, jer će se tom brzinom prostirati i impuls koji je zadat na jednom kraju. Dakle, ako kažeš "apsolutno krut štap" i pri tome definišeš da je brzina prostiranja zvučnih talasa u njemu beskonačna - imaš svoj odgovor. S druge strane, ako pretpostaviš da je brzina prostiranja zvuka kroz štap konačna, tad impuls stiže nakon određenog vremena na drugi kraj, pri čemu je štap kraći dok impuls putuje duž njega.

Dakle, odgovor se krije u samoj pretpostavci.

"I'd take the awe of understanding over the awe of ignorance any day."
- Douglas Adams

Odgovor na temu

Shadowed
Vojvodina

Član broj: 649
Poruke: 12881

+4827 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{19.04.2007. u 15:14 - pre 219 meseci}

Problem je u postavci.
Idealno krut stap je aproksimacija. Kao i druge aproksimacije, u nekim situacijama je razlika izmedju stvarnih i aprosimativnih vrednosti zanemarljiva ali u nekim nije. U ovom slucaju nije. Upravo to sto si taj stap ucinio drugacijim nego sto u prirodi moze biti si situaciju napravio nemogucom.
U realnosti bi se naravno, smanjilo rastojanje izmedju atoma prvo na tvom kraju pa zatim malo dalje, pa jos dalje, dok bi na tvom kraju pocelo da se vraca to rastojanje na stavu vrednost. Konkretno - imao bi neku vrstu talasa.

Nebojsa Milanovic:
-Trumpa smatram vrhunskim predsednikom i voleo bih da živim u državi na čijem je on čelu
-Rusija ne laže, ne vodi osvajačke ratove
-Trump je svetla tačka u USA blatu
-Elon Musk, možda najpametniji i najtrezveniji Amerikanac

Odgovor na temu

Milan Milosevic

Član broj: 67
Poruke: 932
77.46.225.*

+31 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{19.04.2007. u 16:42 - pre 219 meseci}

Izvrsice se kontrakcija duzine stapa sa sopstveni sistem posmatraca iako je on idealno krut. A poremecaj ce se preneti posle 1 s.

Odgovor na temu

pctel
Beograd

Član broj: 13030
Poruke: 10908

+1351 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{19.04.2007. u 17:12 - pre 219 meseci}

Citat:

tražio sam odgovor kod raznih ljudi (među kojima je bilo i profesora fizike), ali ne samo da su odgovori bili prilično različiti, nego nisu bili ni dovoljno uverljivi

Problem razlicitih odgovora lezi u tome sto odgovor zavisi od tacke posmatranja. Evo ti 3 primera:

- posmatrano iz tvog polozaja, drugi kraj ce se pomeriti sekundu kasnije nego sto si ga gurnuo
- posmatrano iz polozaja tvog pomocnika, pomerice se sekundu ranije nego sto si ga gurnuo
- posmatrano sa sredine stapa, pomerice se istog trenutka kad si ga gurnuo.

Samo ti sinko (administratore) radi svoj posao.

Odgovor na temu

Milan Milosevic

Član broj: 67
Poruke: 932
77.46.225.*

+31 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{19.04.2007. u 18:08 - pre 219 meseci}

Da kontrakcija duzine nije vezana za fizicku deformaciju stapa vec za sistem iz koga se posmatra. Potrazi negde u literaturi gde je detaljnije objasnjena kontrakcije duzine i videces da se i tu duzina stapa iz sopstvenog sistema reference stapa tretira takode kao nepromenjiva.

Odgovor na temu

Daniel011
Beograd

Član broj: 76088
Poruke: 1101
*.dynamic.sbb.co.yu.

ICQ: 2336441

+3 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{19.04.2007. u 20:10 - pre 219 meseci}

Eto, za sada imamo tri različita objašnjenja ove "zagonetke".

@Not_now,_John! & @Shadowed
Objašnjenje koje ste vi dali mi nije bilo ponuđeno za ovih 15 godina koliko sam se raspitivao, a upravo taj mehanizam mi se čini najlogičnijim. Znači, pomeraj se prenosi kao talas, a rezultat je da se drugi kraj štapa neće pomeriti ni istovremeno, ni posle jedne sekunde, nego će se pomeriti posle onoliko vremena koliko je zvuku potrebno da, krećući se kroz taj štap, pređe razdaljinu od 300,000km. Right?

Citat:

Milan Milosevic: Izvrsice se kontrakcija duzine stapa sa sopstveni sistem posmatraca iako je on idealno krut. A poremecaj ce se preneti posle 1 s.

Ovo objašnjenje sa kontrakcijom dužine štapa mi je ponudio jedan profesor fizike na ETF-u (nažalost, sada već pokojni). Međutim, u tom pristupu, koliko se meni čini, ima nekih nelogičnosti. Kontrakcija dužine se dešava pri kretanju nekog tela brzinom koja je bliska brzini svetlosti. Ja štap ipak pomeram nekom brzinom koja je zanemarljiva u odnosu na brzinu svetlosti. Slažem se i da je ta kontrakcija od par cm (za koliko sam ga pomerio) zanemarljiva u odnosu na dužinu štapa od 300,000km, međutim, kontrakcija zavisi od brzine kojom ja pomerim štap, a ja ga mogu pomerati i brže i sporije, pa da kontrakcija ne bude ista u ta dva slučaja. Osim toga, mogu štap pomeriti istom brzinom i za 1cm, a i za 5cm, pri čemu kontrakcija mora u oba slučaja biti ista jer je brzina pomeranja ista.

Evo primera sa pretpostavljenim brojnim vrednostima: štap pomeram za

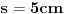
. Vreme koje mi je potrebno da načinim taj pomeraj je

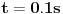
. Dužina štapa je, kao što znamo,

.

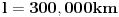
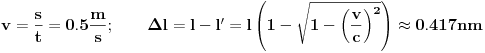
Znači, kontrakcija dužine štapa će iznositi manje od pola nanometra! U poređenju sa tih 5cm za koliko sam pomerio štap, to je zaista zanemarljiva pojava.

Citat:

pctel: Problem razlicitih odgovora lezi u tome sto odgovor zavisi od tacke posmatranja. Evo ti 3 primera:

- posmatrano iz tvog polozaja, drugi kraj ce se pomeriti sekundu kasnije nego sto si ga gurnuo
- posmatrano iz polozaja tvog pomocnika, pomerice se sekundu ranije nego sto si ga gurnuo
- posmatrano sa sredine stapa, pomerice se istog trenutka kad si ga gurnuo.

Ti ovime nisi ponudio različite odgovore, nego se tvoj odgovor svodi na jednu tvrdnju - da se štap na oba svoja kraja pomeri istovremeno (a kako ćemo mi to videti iz kog mesta posmatranja, to je druga stvar). Zapravo, ovo što ti tvrdiš je ono što sam ja napisao kao mogućnost pod 1).
Slažeš li se da tvoja tvrdnja znači da je informacije moguće slati beskonačno velikom brzinom?

Odgovor na temu

Milan Milosevic

Član broj: 67
Poruke: 932
77.46.225.*

+31 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{20.04.2007. u 07:06 - pre 219 meseci}

Najpre treba da definisemo kako se odreduje duzina stapa da kasnije oko toga ne bude zabune. Duzina stapa se odreduje merenjem. Odnosno uporedivanjem pocetne i krajnje tacke stapa. Informacija do posmatraca se prenosi putem svetlosti dakle konacnom brzinom. U trenutku pomeranja stapa blizi kraj ka posmatracu je pomeren za neku vrednost Δl.Zbog blizine mi taj pomeraj vidimo trenutno.Medutim u tom trenutku informacija koju dobijamo o udaljenom kraju stapa zbog konacne brzine svetlosti je ona koju je stap imao pre pomeranja. Dakle mi cemo izmeriti duzinu stapa l-Δl.Tek nakon vremenskog intervala Δt=l/c=1s
mi cemo da registrujemo da se duzina stapa vratila na duzinu l.Dakle za posmatraca pomeraj putuje brzinom c iako se stap pomera neznatnom brzinom.
Za posmatraca na drugom kraju imamo prividno povecanje duzine u periodu 1 s

Odgovor na temu

pctel
Beograd

Član broj: 13030
Poruke: 10908

+1351 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{20.04.2007. u 10:27 - pre 219 meseci}

Citat:

Ti ovime nisi ponudio različite odgovore, nego se tvoj odgovor svodi na jednu tvrdnju - da se štap na oba svoja kraja pomeri istovremeno (a kako ćemo mi to videti iz kog mesta posmatranja, to je druga stvar).

Ako hoces da ukljucis teoriju relativiteta, onda svejedno ne mozes zanemariti tacku posmatranja - duzina stapa ce zavisiti od tacke posmatranja, znaci upravo pricamo o tome kako cemo mi to videti, ono sto se stvarno desava je nebitno za teoriju relativiteta.

Citat:

Slažeš li se da tvoja tvrdnja znači da je informacije moguće slati beskonačno velikom brzinom?

Pa zavisi kako se uzme... ako dodje do kontrakcije duzine, stap nece biti dug 300.000 km, vec recimo 1 km, a vreme nece biti 0.00000....0000000001 sekunda, vec recimo 0.000003 sekunde, pa kad sa takvim podacima izracunas brzinu prenosa informacije opet ces dobiti da je ona 300.000 km u sekundi.

Citat:

Kontrakcija dužine se dešava pri kretanju nekog tela brzinom koja je bliska brzini svetlosti. Ja štap ipak pomeram nekom brzinom koja je zanemarljiva u odnosu na brzinu svetlosti.

Da, ali pricas o brzini prenosa informacije o pomeranju stapa, koja je veoma bliska brzini svetlosti.

Samo ti sinko (administratore) radi svoj posao.

Odgovor na temu

Shadowed
Vojvodina

Član broj: 649
Poruke: 12881

+4827 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{20.04.2007. u 11:27 - pre 219 meseci}

Citat:

pctel: Ako hoces da ukljucis teoriju relativiteta, onda svejedno ne mozes zanemariti tacku posmatranja - duzina stapa ce zavisiti od tacke posmatranja, znaci upravo pricamo o tome kako cemo mi to videti, ono sto se stvarno desava je nebitno za teoriju relativiteta.

Ovo je razlog zasto sam ja prestao da se interesujem za ove stvari. Mislim da bi fizika trebala da se bavi onim sto se stvarno desava a ne (samo) onim sto mi vidimo.

Nebojsa Milanovic:
-Trumpa smatram vrhunskim predsednikom i voleo bih da živim u državi na čijem je on čelu
-Rusija ne laže, ne vodi osvajačke ratove
-Trump je svetla tačka u USA blatu
-Elon Musk, možda najpametniji i najtrezveniji Amerikanac

Odgovor na temu

Daniel011
Beograd

Član broj: 76088
Poruke: 1101
*.dynamic.sbb.co.yu.

ICQ: 2336441

+3 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{20.04.2007. u 11:42 - pre 219 meseci}

@Milan Milosevic & @pctel

Mislim da se nismo najbolje razumeli oko suštine mog pitanja. Pokušaću zato da pitanje postavim malko drugačije.

Za početak, zamislimo da pomoćnik i ja (koji smo udaljeni 300,000km) nemamo štap, nego informacije razmenjujemo dizanjem i spuštanjem ruku. Ja recimo podignem svoju ruku i u momentu kad pomoćnik registruje da sam podigao ruku, prema ranijem dogovoru, on odmah podigne svoju (pretpostavimo da imamo beskonačno brze reflekse). Da li se slažete da će od momenta mog podizanja ruke pa do momenta kad ću ja videti da je pomoćnik podigao svoju ruku, proći dve sekunde? Od momenta mog podizanja ruke mora prvo da prođe jedna sekunda da bi ta svetlost došla do pomoćnika i da bi on to video i podigao svoju ruku, a zatim opet jedna sekunda da bih ja registrovao da je pomoćnik odgovorio podizanjem ruke. Znači, dve sekunde. To je i logično, jer informacija (u koju ubrajamo i moje i njegovo podizanje ruku) je prešla ukupan put od 600,000km. A upravo brzina svetlosti je i max. brzina prenosa informacije (kao i bilo čeka drugog u univerzumu).

Nadam se da u vezi prethodnog slučaja nema nedoumica i da se sa time slažemo.

E sad se vratimo na štap. Neka je dogovor takav da onog momenta kad pomoćnik primeti da se štap pomerio, on podigne ruku. Pitanje je: koliko će vremena proći od trenutka kada sam pomerio štap do trenutka kada ću videti da je pomoćnik podigao ruku?

Ili ako zamislimo slučaj da pomoćnik i ja ne komuniciramo pomeranjem ruku, nego isključivo pomeranjem štapa... Ja pomerim štap na svom kraju, on čim to registruje odmah odgovori takođe pomeranjem štapa (opet radi pojednostavljenja zanemarujemo kašnjenje zbog konačne brzine refleksa). Koliko će u ovom slučaju proći vremena od trenutka kad sam pomerio štap do trenutka kad registrujem pomeranje svog kraja štapa, kao pomoćnikov odgovor?

Odgovor na temu

McKracken
Vladimir Jovanovic
HuxleyDev

Član broj: 465
Poruke: 2941
*.dhcp-pool-ue.sbb.co.yu.

ICQ: 203079925

+7 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{20.04.2007. u 15:05 - pre 219 meseci}

Citat:

Slažeš li se da tvoja tvrdnja znači da je informacije moguće slati beskonačno velikom brzinom?

Ovo se zove zakljucivanje non-sequitur. Isto bi bilo i kad bi rekao da imamo dve rupe na 300k km i
onda ubacimo informaciju u jednu a on ispadne iz druge.

Odgovor na temu

Daniel011
Beograd

Član broj: 76088
Poruke: 1101
*.dynamic.sbb.co.yu.

ICQ: 2336441

+3 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{20.04.2007. u 15:32 - pre 219 meseci}

Moj zaključak je zasnovan na onome što je čovek rekao:

Citat:

pctel:
- posmatrano iz tvog polozaja, drugi kraj ce se pomeriti sekundu kasnije nego sto si ga gurnuo
- posmatrano iz polozaja tvog pomocnika, pomerice se sekundu ranije nego sto si ga gurnuo
- posmatrano sa sredine stapa, pomerice se istog trenutka kad si ga gurnuo.

Ako pomoćnik vidi da se štap pomerio 1 sekundu pre nego što vidi da sam ja, koji sam udaljen 300,000km, taj štap gurnuo, zaključak je upravo to što sam i napisao: pošto pomoćnik vidi da sam ja gurnuo štap jednu sekundu kasnije nego što sam ga zaista gurnuo (zbog kašnjenja svetlosti), a pomeraj štapa registruje 1 sekundu pre toga, znači da se njegov kraj štapa pomera istovremeno kada i ja pomerim svoj kraj štapa, tj. da se informacija prenosi beskonačnom brzinom, a što je, po meni, nemoguće.
Ako sam u ovom rezonu na nekom mestu pogrešio, molio bih da mi se tačno ukaže na mesto u kome je greška.

Citat:

McKracken: Isto bi bilo i kad bi rekao da imamo dve rupe na 300k km i
onda ubacimo informaciju u jednu a on ispadne iz druge.

Nažalost, ni posle više čitanja ove rečenice nisam uspeo da razumem šta si ovime hteo reći, pa bih bio zahvalan ako možeš malo to da pojasniš.

Odgovor na temu

Milan Milosevic

Član broj: 67
Poruke: 932
77.46.225.*

+31 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{20.04.2007. u 15:59 - pre 219 meseci}

Sto se tice dizanja ruku odgovor je jasan 2 s. A ovaj drugi slucaj nije tako komplikovan kao sto mislis.Ako stap pomeras malim ne relativistickim brzinama
Tada je vreme odredenjo pod uslovom da ti saradnik gura stap istom brzinom nazad t=2 ΔL/v gde je brzina v brzina pomeranja stapa. vreme t koje ovde dobijes imace konacne merljive vrednosti. Nikako beskonacno male.

Odgovor na temu

Daniel011
Beograd

Član broj: 76088
Poruke: 1101
*.dynamic.sbb.co.yu.

ICQ: 2336441

+3 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{20.04.2007. u 16:07 - pre 219 meseci}

OK, ovako kako si objasnio, vreme t će imati konačne merljive vrednosti, to se slažem.
Ali te konačne merljive vrednosti će biti manje od onog vremena koje je svetlosti potrebno da ode od mene do pomoćnika i zatim nazad do mene? Da li se i to slažemo? To se direktno vidi iz ovog što si napisao.
To bi značilo upravo ovo što mene buni, a to je da sledi da je moguće da informaciija putuje brzinom, koja eto nije beskonačna, ali je ipak veća od brzine svetlosti??

Odgovor na temu

McKracken
Vladimir Jovanovic
HuxleyDev

Član broj: 465
Poruke: 2941
*.dhcp-pool-ue.sbb.co.yu.

ICQ: 203079925

+7 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{20.04.2007. u 16:29 - pre 219 meseci}

Ono sto hocu da kazem je da u ovom slucaju ti postavljas pretpostavku da ce se neki objekat ponasati kao idealno krut (homogen i nedeformabilan)
Takva aproksimacija suvise kvari model da bi on imao smisla pa i ono sto se moze zakljuciti iz tog modela nema smisla.

Citat:

To bi značilo upravo ovo što mene buni, a to je da sledi da je moguće da informaciija putuje brzinom, koja eto nije beskonačna, ali je ipak veća od brzine svetlosti??

Greska u zakljucivanju :)

http://www.nizkor.org/features/fallacies/

Odgovor na temu

Milan Milosevic

Član broj: 67
Poruke: 932
77.46.225.*

+31 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{20.04.2007. u 16:34 - pre 219 meseci}

Pa to nije informacija koja putuje do tvog pomocnika vec informacija koja putuje ispred tebe do tvog kraja stapa.Jer ti posmatras samo svoj kraj i pomocnik svoj.

Odgovor na temu

vaske71

Član broj: 61960
Poruke: 1438
77.46.225.*

+109 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{20.04.2007. u 17:23 - pre 219 meseci}

Nikako se ne moze zamisliti krut stap navedene duzine a odgovor na ovo pitanje je da stapa uopste i nema
Zamisli da si ti foton i da putujes navedenom brzinom od tacke A (pocetak stapa) do tacke B (kraj stapa) a sa navedenom jedinicom vremena od 1 sec - sledi prosto objasnjejnje da za navedeni period vremena uopste nisi mogao da vidis stap po kome se kreces a da bi ga i u mislima uopste video (pod navedenom brzinom) moraces da uzmes i trecu tacku C, kojoj ces da normalno postavis na stap u svom vidnom horizontu - Kada duzinu umanjis tj stavis trecu tacku a na 20 km i umanjis BRZINU svog kretanja u mislima za oko 15 000 puta videces da stap nije uopste APSOLUTNO PRAV - vec KRIV
Sledi da Bilo koja "prava " a za duzinu tvog najduzeg vidnog polja -Nije PRAVA - mora imati zakrivljenost !!!
Apsolutno PRAV stap nije i ne moze biti a da putujes po njemu u bilo kom pravcu !!!

Zamisljenost pitanja o stapu nema dovoljan period vremena za resenje !!!

Odgovor na temu

Vladokv
Vladimir Knezevic
Svuda po gradu
Sopstvena Gewerbe
Berlin

Član broj: 31521
Poruke: 478
212.62.39.*

Sajt: goo.gl/ZbvDC

+16 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{20.04.2007. u 18:15 - pre 219 meseci}

Moje mišljenje je da će se pomeraj desiti sa kašnjenjem od jedne sekunde. Ako napravimo analogiju sa el. strujom trebalo bi da bude tako.
Struja je usmereno i jako sporo kretanje elektrona(cm u sekundi ili manje zavisno od jačine struje).Ali njeno dejstvo - prenos poremećaja, kao što je dovođenje napona se prenosi brzinom svetlosti.

Odgovor na temu

Daniel011
Beograd

Član broj: 76088
Poruke: 1101
*.dynamic.sbb.co.yu.

ICQ: 2336441

+3 Profil

Re: Misaoni eksperiment - štap dužine 300,000km

^{20.04.2007. u 18:52 - pre 219 meseci}

Ova rasprava je svojim tokom krenula u sasvim drugom pravcu... Odgovor koji su mi u startu dali Not_now,_John! i Shadowed deluje mi sasvim logičan i prilično sam ubeđen da je upravo to pravo objašnjenje. Prema tome, što se mene tiče, na samo moje pitanje šta se dešava sa štapom, može se staviti tačka.

Ali zaista me čudi da se ovde iznose shvatanja po kojima se pomeraj štapa prenosi na drugi kraj trenutno, a da, pritom, to ne znači da se informacija prenosi brzinom većom od c. Ljudi, dovoljno je da samo malo razmislite, nije teško shvatiti. Ja sam mogao sa mojim pomoćnikom da se dogovorim sledeće: na moj prvi pomeraj štapa, ti mi uzvrati jednim pomerajem ako kod tebe sija sunce, a uzvrati sa dva pomeraja ako kod tebe pada kiša. Zatim, na moj sledeći pomeraj štapa, ti uzvrati jednim pomerajem ako je tamo kod tebe na izborima pobedio demokratski blok, a uzvrati sa dva pomeraja ako je pobedio onaj drugi blok. I svi ti pomeraji, ako imamo dovoljno brze reflekse, mogu se obaviti ukupno za sekundu. Bilo kojim drugim načinom komunikacije, svetlošću, radio-talasima, ili nekim drugim načinom pri čemu se te informacije prenose brzinom svetlosti, trebalo bi nam bar 4 sekunde (po dva puta u oba smera).

Vladokv, slažem se s tvojim načinom razmišljanja, samo još ostaje pitanje da li se u tom štapu poremećaj prenosi onom brzinom kojom se kroz taj štap prostire zvuk, kako je to rekao Not_now,_John!, ili se prenosi brzinom svetlosti, kao što ti kažeš.

Odgovor na temu

[es] :: Fizika :: Misaoni eksperiment - štap dužine 300,000km

Strane: 1 2

[ Pregleda: 5623 | Odgovora: 22 ] > FB > Twit

Srodne teme

26.06.2004. Moram uzeti neki olympus do 600 KM (300Eura), koj..
18.07.2004. 1.PC WIN XP sa PRINTEROM HP 1100 2.PC WIN NT. Št..
04.02.2005. Veliki broj provera dužine pesama
28.04.2005. Legenda o Hanojskim kulama
04.05.2005. WinXP na 300 MHz
20.12.2010. Elektronski regulator temperature do 300 stepeni
28.10.2005. Spajanje kabelske televizije u zgradi
09.04.2006. Golf 2 1.6 TD Neravnomeran rad motora
05.10.2006. Epson LX-300+ problem sa logickom plocom
12.11.2009. Dimenzije pločice za UNIVERSAL P-300

Navigacija

Lista poslednjih: 16, 32, 64, 128 poruka.