Tu sam ja, samo vas gledam
Pratim temu, nisam se izgubio, ali nikako nisam imao vremena da se javljam jer sam trenutno rastrzan između više ispita tako da ne znam na koju ću stranu pre.
Problem sam uspeo da rešim ali samo delimično.
Naime, ove linearne jednačine sa parametrima imam za ispit, međutim zbirka iz koje vežbam (koja inače sadrži ispitne zadatke iz prethodnih rokova) nema rešenja sa sve zadatke, tako da mi je bio potreban softver koji će mi služiti za proveru da li tačno rešavam zadatke. Nekako sam se ipak snašao, a pre svega zahvaljujući konstruktivnom predlogu od strane
Djomlouna kome se ovom prilikom zahvaljujem, tako što sam "izbildovao" listu jednačina u zavisnosti od parametara. Mi na fakultetu (FON), ove sisteme rešavamo pomoću matrica, tj. matrice sistema i proširene matrice sistema, pa se onda vrši redukcija tj. oduzimanje ili sabiranje između pojedinih vrsta(redova) matrica, u zavisnosti šta je potrebno. Da ne objašnjavam dalje shvatiće oni koji su imali muke sa ovim sistemima. Kažem "mi tako rešavamo", jer nisam neki matematičar, pa ne znam da li postoje drugi načini rešavanja.
E sad evo jednog primera.
x + 2y - 3z + 4u = -1
x + 2ay + 7z + 10u = -5
(a-1)y + (b+3)z + (a+2)u = b-4 , gde su a i b realni parametri
Prvo sam rešio jednačinu, pa sam je onda proveravao, tj. sve vrednosti posebno za svaki parametar.
Neka je A matrica sistema, a A* proširena matrica sistema, tada A* ima oblik:
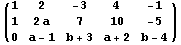
Kada se prva vrsta (red) doda drugoj vrsti pomnožena sa -1, tj. kada se od druge vrste oduzme prva, onda imamo:
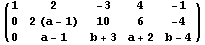
Sada se druga vrsta podeli sa 2, i onda je:
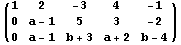
Sada trećoj vrsti dodamo drugu pomnoženu sa -1 i konačno dobijamo:
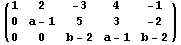
E sada razmatramo moguće slučajeve.
-1) Ako je a različito od 1, tada je r(A)=r(A*)=3, sistem je saglasan i ima jednoparametarski skup rešenja. Evo kako to izgleda u Mathematici:
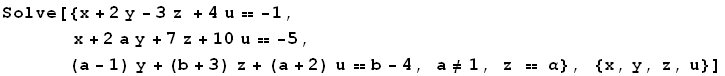
onda sam pritisnuo Shift+Enter i dobio sledeće rešenje:
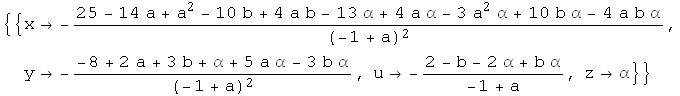
E sad nastupa "sex", jer ovde dobijam rešenje u drugačijem obliku od onog koje sam ja dobio. Imam dva moguća izbora: da uzmem papir i olovku i da upoređujem sam da li je moje rešenje identično sa onim koje mi je izbacila Mathematica ili da prodžaram po helpu i nađem foru da Mathematica to uradi umesto mene. Odlučujem se ipak za ovo drugo i nakon dosta cimanja uspevam da pronađem foru:
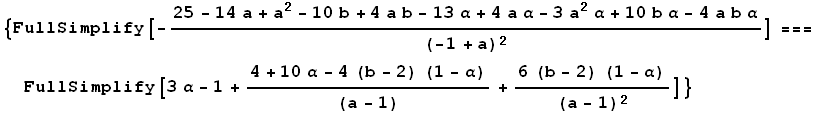
da ne objašnjavam mnogo, izraz sa leve strane je onaj koji je izbacila Mathematica a izraz sa desne strane je ono što sam ja dobio za X. Onda Shift+Enter i dobijam odgovor:
(nastaviće se...)
[Ovu poruku je menjao radeg dana 04.04.2007. u 16:07 GMT+1]
Mathematica 5.1 i sistemi linearnih algebarskih jednačina
