Evo još jednog dokaza da menjanje odluke ne uvećava šansu za odabir prave koverte. Ovog puta sam dokaz izveo koristeći pomenutu Bayes-ovu formulu, na taj način što sam zadatak sa crvenim, zelenim i plavim vratima, koji je Braker postavio u attachmentu, preveo i prepravio tako da odgovara ovom našem slučaju sa kovertama. Izmene su bile neminovne, s obzirom da početni uslovi u ova dva zadatka, iako na prvi pogled deluju identični, ipak to nisu.
Na raspolaganju su tri koverte - crvena, zelena i plava - od kojih jedna u sebi sadrži nagradu. Izabiramo crvenu kovertu. Žena koja prva izvlači kovertu i pri tom ne zna u kojoj koverti je nagrada, kao što ne zna ni koju smo kovertu mi izabrali, izvlači zelenu kovertu. Pod pretpostavkom da u toj koverti nema nagrade, koja je verovatnoća da je nagrada u plavoj koverti?
Nazovimo situaciju u kojoj je nagrada u datoj koverti
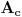
,
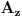
,
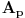
. (c-crvena, z-zelena, p-plava)
Za početak,
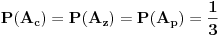
i, kako bismo uprostili stvari, pretpostavimo da smo već u mislima izabrali ("pikirali") crvenu kovertu.
Nazovimo

"prva žena izvlači zelenu kovertu". Bez ikakvog prethodnog znanja, ovom događaju pridružujemo vrednost verovatnoće
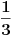
.
- u situaciji da je nagrada u crvenoj koverti, prva žena izvlači crvenu, zelenu ili plavu kovertu, po slučajnom izboru. Dakle,
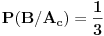
- u situaciji da je nagrada u zelenoj koverti, prva žena izvlači crvenu, zelenu ili plavu kovertu, po slučajnom izboru. Dakle,
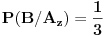
- u situaciji da je nagrada u plavoj koverti, prva žena izvlači crvenu, zelenu ili plavu kovertu, po slučajnom izboru. Dakle,
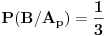
Dakle,
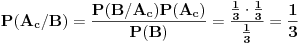
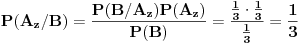
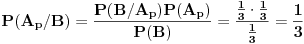
To bi bila "prepravka" attachovanog zadatka sa vratima, tako da odgovara našem slučaju sa kovertama. Kao što se vidi, ništa posebno ovime nije dokazano. Pokazano je samo to, da je posle izvlačenja zelene koverte od strane prve žene, ali
pre otvaranja te zelene koverte, verovatnoća da je nagrada u bilo kojoj od koverata, ista za sve tri koverte i iznosi
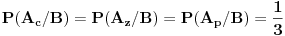
.
Zatim dalje proširujemo postupak: sada kad je poznato da je prva žena izvukla zelenu kovertu, tj. da više nije neizvesno koju će kovertu ona izvući, uvodimo događaj da se u toj zelenoj koverti ne nalazi nagrada, tj. da prva žena ostaje bez nagrade i taj događaj nazovemo

. Očigledno je da je
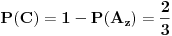
- u situaciji da je nagrada u crvenoj koverti, prva žena izvlačenjem zelene koverte 100% ostaje bez nagrade. Dakle,
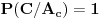
- u situaciji da je nagrada u zelenoj koverti, prva žena izvlačenjem zelene koverte nikako ne može ostati bez nagrade. Dakle,
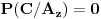
- u situaciji da je nagrada u plavoj koverti, prva žena izvlačenjem zelene koverte 100% ostaje bez nagrade. Dakle,
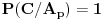
Dakle,
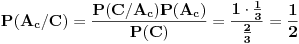
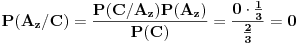
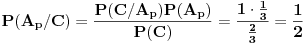 Zaključak: kada se desio događaj
Zaključak: kada se desio događaj  , tj. prva žena izvukla zelenu kovertu, otvorila je i konstatovala da se u njoj ne nalazi nagrada, verovatnoće
, tj. prva žena izvukla zelenu kovertu, otvorila je i konstatovala da se u njoj ne nalazi nagrada, verovatnoće 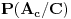 i
i 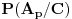 da je nagrada u crvenoj, odnosno plavoj koverti, su jednake i iznose
da je nagrada u crvenoj, odnosno plavoj koverti, su jednake i iznose 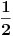 .
.