Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.

evo jedan zadatak iz (elementarne??) geometrije

[es] :: Matematika :: evo jedan zadatak iz (elementarne??) geometrije

[ Pregleda: 4007 | Odgovora: 14 ] > FB > Twit

Postavi temu Odgovori

Autor
Pretraga teme: Traži
Markiranje Štampanje RSS

badzevic

Član broj: 13299
Poruke: 29
*.dynamic.sbb.co.yu.



Profil

icon evo jedan zadatak iz (elementarne??) geometrije06.12.2006. u 06:42 - pre 223 meseci
pozdrav svima

Neka su dati kruznica k, prava p i tacka A van p. Na pravoj p konstruisati tacku P takvu da je |AP|=|PT|, gde je T dodirna tacka kruznice k i tangente na nju povucene iz P.

mozda gresim ali cini mi se kao jako tesko

ima li neko inspiraciju
Keep On Keepin' On
 
Odgovor na temu

braker

Član broj: 80035
Poruke: 419
*.smin.sezampro.yu.



+2 Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije06.12.2006. u 10:49 - pre 223 meseci
Izgleda da mogucnost reshavanja zavisi od izbora tachaka A i T,kao i polozhaja prave p,pa povedi rachuna:)
Uglavnom,mislim da je moguce reshiti zadatak na sledeci nachin:

Spojish tachke A i T,nadjesh simetralu duzhi AT,iz te tachke (polovina duzhi AT) normalno na AT povuchesh liniju-mesto preseka sa pravom p daje tachku P.
.
 
Odgovor na temu

badzevic

Član broj: 13299
Poruke: 29
*.dynamic.sbb.co.yu.



Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije06.12.2006. u 18:54 - pre 223 meseci
nisi pazljivo citao

tacka T nije data

tacka T je jednostavno dodirna tacka kruga i tangente koja se povlaci iz tacke P koju treba konstruisati

dakle treba naci P na zadatoj pravoj p takvu da je odstojanje od dodirne tacke na tangenti jednako odstojanju od zadate tacke A

nisam sposoban ovo da resim
Keep On Keepin' On
 
Odgovor na temu

badzevic

Član broj: 13299
Poruke: 29
*.dynamic.sbb.co.yu.



Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije07.12.2006. u 00:41 - pre 223 meseci
ah

uz omanje konsultacije pojavilo se elegantno resenje

inverzija u odnosu na krug. preslikamo li tacku A inverzno u odnosu na k dobijamo tacku A'. buduci da inverzija ostavlja invarijantne kruznice koje su normalne na k, takva ce biti kruznica k' koja sadrzi A i A'.

sada se zadatak svodi na konstruisanje k' jer su u njenoj presecnoj tacki sa k poluprecinici od k i k' ortogonalni pa je ta tacka upravo tacka T tj taj polucprecnik od k' je upravo tangenta od k

zato je centar k' upravo trazena tacka P jer je tada |TP|=|PA|

da bismo konstruisali k' potrebna nam je jos jedna tacka, pa posto zelimo da P pripada p, jednostavno cemo A preslikati simetricno u odnosu na p i tako dobiti A''

tako je k' odredjena tackama A, A' i A'', tj P se nalazi u preseku prave p i simetrale duzi A'A''


evo radosti za one koji su se zainteresovali za ovaj zadatak (ukoliko ih ima)
Keep On Keepin' On
 
Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.ADSL.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253


+621 Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije09.12.2006. u 16:22 - pre 223 meseci
Evo sličnog zadatka, rešenje prethodnog je stvarno lepo bila bi šteta da se brzo izgubi. :)

Zadatak 2:

Dato je: kružnica , tačka , ugao . Naći tačku takvu da je , gde je dodirna tačka kružnice i tangente na nju povučene iz , pri čemu je .

Kome je ovo lagano može da proba i malo zakomplikovanu verziju.

Zadatak 3:

Dato je: kružnice i , ugao . Naći tačku takvu da je , gde su i dodirne tačke kružnica i i tangenta na njih povučenih iz , redom, pri čemu je .
Ljubičice crvena, što si plava kô zelena trava.
 
Odgovor na temu

badzevic

Član broj: 13299
Poruke: 29
*.dynamic.sbb.co.yu.



Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije09.12.2006. u 18:07 - pre 223 meseci
evo na brzaka samo da odgovorim na prvi izazov drugi ce sacekati kad budem imao vise vremena

zadrzacemo iste oznake, samo je mala varijacija na temu, isto konstruisemo A' inverzijom na krug, uz tu razliku sto k' sada trazimo pod drugim uslovima

kako je prava AA' tetiva trazene kruznice, periferijski ugao nad njom ce biti jednak polovini centralnog, a centralni je upravo dati fi

stoga provlacimo kroz A proizvoljnu pravu, i na nju iz A' spustamo pravu pod uglom od fi/2, neka je njihov presek neka tacka A''

trazena tacka P je sada centar kruga k' odredjenog tackama A, A' i A''

treci zadatak ce dobiti tretman kasnije u toku veceri
Keep On Keepin' On
 
Odgovor na temu

badzevic

Član broj: 13299
Poruke: 29
*.dynamic.sbb.co.yu.



Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije09.12.2006. u 18:30 - pre 223 meseci
ne valja bre ovo

fi je ugao nad tetivom AT, ne AA', brljam

sacekajmo veceras
Keep On Keepin' On
 
Odgovor na temu

badzevic

Član broj: 13299
Poruke: 29
*.dynamic.sbb.co.yu.



Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije09.12.2006. u 18:56 - pre 223 meseci
jel moze ovako

ugao <A'TA je jednak polovini ugla <A'PA, jer su oni centralni i periferijski uglovi hipoteticne kruznice k'

analogno ugao <A'AT je polovina ugla <A'PT

kako je <A'PT + <A'PA = fi, to je <A'TA + <A'AT = fi / 2

pa je ugao <AA'T= pi - fi/2

dakle

inverzijom nalazimo A'

iz A' povlacimo pravu pod uglom pi - fi/2 u odnosu na pravu AA'

tacka T je tada presek ove prave sa kruznicom k

sada je trazena tacka P srediste kruznice k' odredjene tackama A, A' i T


da li sam opet nesto zabrljao?
Keep On Keepin' On
 
Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.ADSL.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253


+621 Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije09.12.2006. u 19:26 - pre 223 meseci
Sad je OK (ako nisam i ja nešto prevideo). Ostaje treći zadatak (da napomenem, postoji i četvrti, za kraj ).
Ljubičice crvena, što si plava kô zelena trava.
 
Odgovor na temu

badzevic

Član broj: 13299
Poruke: 29
*.dynamic.sbb.co.yu.



Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije10.12.2006. u 16:49 - pre 223 meseci
sve mi se nesto cini da resenje zadatka broj 3 (ko li ga je smislio) nije jednoznacno, vec ih avaj ima beskonacno

probacu da poduprem ovo

preslikajmo kruznicu k2 inverzijom u odnosu na k1, dobijamo kruznicu k2'. slika od PA, tangente k2, ce biti neka kruznica, obelezimo je sa Kpa, koja ce dodirivati k2' i prolaziti kroz centar inverzije O.

upravo u ovom trenutku mi se cini da lezi uzrok viseznacnosti resenja, jer izgleda da je izbor takve kruznice proizvoljan, dok god cela lezi unutar k1, a takvih ima i dalje beskonacno mnogo

slika tangente na k1, PT, bice takodje kruznica, obelezicemo je sa Kpt, koja iznutra dodiruje k1 u tacki T i prolazi kroz O, ali takodje se i sece sa Kpa pod uglom fi, jer ako se ne varam kruzna inverzija cuva uglove

konstrukcija dakle tece ovako, nakon sto smo preslikali k2 i uzeli proizvoljno Kpa (ali takvu da je unutar k1), povlacimo na nju tangentu t iz O, i zatim takodje iz O, pravu p pod uglom fi u odnosu na t

prava p je sada tangenta kruznice Kpt u tacki O, kruznice koja treba da dodiruje iznutra k1, pa zato povlacimo normalu na p u O i u njenom preseku sa k1 dobijamo tacku T

centar od Kpt je zato polovina duzi OT

druga presecna tacka tako dobijenih kruznica Kpa i Kpt (pored O koja i ionako ne figurise jer nema konacnu inverznu sliku) bice slika P' trazene tacke P, pa dakle resenje nalazimo inverznim preslikavanjem tacke P' u odnosu na k1

ukoliko ova prica ima smisla, najavljeni zadatak broj 4 bi mogao da glasi ovako:

koju krivu predstavlja geometrijsko mesto svih tacaka P sa trazenim svojstvima?
Keep On Keepin' On
 
Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.ADSL.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253


+621 Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije10.12.2006. u 18:15 - pre 223 meseci
Ne valja baš. Nigde se nisi obezbedio da bude .
Ljubičice crvena, što si plava kô zelena trava.
 
Odgovor na temu

badzevic

Član broj: 13299
Poruke: 29
*.dynamic.sbb.co.yu.



Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije11.12.2006. u 20:30 - pre 223 meseci
mmmm da.. jes tacno

i k2 i k2' sadrze po tacku koja se nalazi na kruznici k' koju jurim da konstruisem, ali nista mi ne garantuje da je jedna od njih slika one druge, a to se mora desiti

znaci radio bih jos na ovome ali moram priznati da u ovom slucaju znatizelja nadjacava strpljenje

stoga ajde, cujmo resenje

fusnota: znaci li ovo da je resenje ipak jednoznacno?
Keep On Keepin' On
 
Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.ADSL.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253


+621 Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije12.12.2006. u 11:23 - pre 222 meseci
Nema problema, onda ću odmah dati rešenje četvrtog zadatka, koji je samo uopštenje trećeg pa se ova konstrukcija može primeniti i na njega (a i na drugi, koji je specijalan slučaj trećeg).

Zadatak 4:

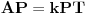
Dato je: kružnice i , ugao , realan broj . Naći tačku takvu da je , gde su i dodirne tačke kružnica i i tangenta na njih povučenih iz , redom, pri čemu je .

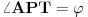
Rešenje:

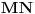
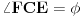
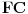
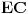
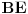
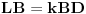
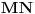
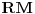
Neka su i centri kružnica i , redom. Iz proizvoljne tačke na pravoj povucimo normalu na tu pravu. Iz proizvoljne tačke ove normale konstruišimo ugao (dve mogućnosti). Povucimo sada tangentu u tački , paralelnu sa , na kružnicu (dve mogućnosti); neka ova tangenta seče u . Odaberimo na pravoj tako da je . Nađimo sada na tako da je duž jednaka poluprečniku kružnice (dve mogućnosti). 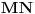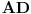Sa centrom u i poluprečnikom , opišimo kružnicu koja seče u (dve mogućnosti). 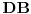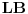Kroz povucimo pravu paralelnu sa , i neka je njen presek sa tačka . 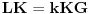Uočimo da je i da je . 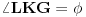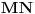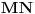Iz povucimo pravu paralelnu sa ; s centrom u tački i poluprečnikom opišimo kružnicu, koja seče ovu pravu u tački . 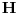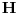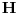Pošto je, za odgovarajući izbor tačke , četvorougao paralelogram, kružnica koja prolazi kroz i s centrom u podudarna je s kružnicom , i nalazi se na istom rastojanju od kružnice . 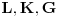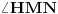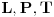Dakle, dovoljno je rotirati tačke oko tačke za , i dobićemo tačke , redom.

Primetimo da ima ukupno šesnaest mogućnosti za ovu konstrukciju. Međutim, posle završne rotacije, neka rešenja će se poklopiti, ostavljajući nam ukupno osam različitih tačaka , u opštem slučaju. Evo slike jedne od njih.



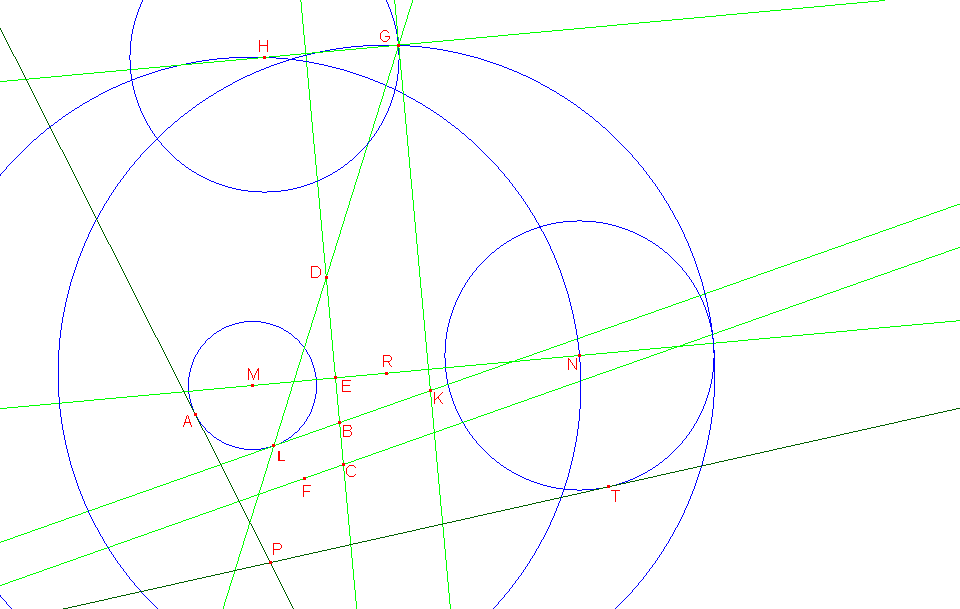
Brzo smo rešili ove zadatke, nisu ni dospeli na listu nerešenih. :)
Ljubičice crvena, što si plava kô zelena trava.
Prikačeni fajlovi
Tangente u datom odnosu.gif Tangente u datom odnosu.gif - 13.27k
 
Odgovor na temu

Tijana
Tijana Zlatkovic
Zajecar

Član broj: 5313
Poruke: 10
213.244.197.*



Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije14.12.2006. u 14:29 - pre 222 meseci
Potrebna mi je pomoc oko zadatka za 6. razred za takmicenje.

U pravouglom trouglu ABC na hipotenuzi AB date su tacke M i N tako da je AM=AC i BN=NC. Odrediti ugao MCN.
Svaki savet bi mi znacio.



Hvala
help me!
 
Odgovor na temu

Farenhajt
Goran Kapetanović
Beograd

Član broj: 78132
Poruke: 449
62.193.129.*



+6 Profil

icon Re: evo jedan zadatak iz (elementarne??) geometrije14.12.2006. u 14:40 - pre 222 meseci
Citat:
Tijana: ...tako da je AM=AC i BN=NC.


Koliko vidim, posredi je greška: Treba da bude .

Uputstva: Kakav je po vrsti ? Ako obeležimo sa , kako će glasiti izraz za ? A kako će onda glasiti izraz za ?

Slično razmatranje primenićemo i na da bismo našli . Kad smo našli ta dva ugla, kako će glasiti izraz za ? Kako taj izraz možemo uprostiti?
 
Odgovor na temu

[es] :: Matematika :: evo jedan zadatak iz (elementarne??) geometrije

[ Pregleda: 4007 | Odgovora: 14 ] > FB > Twit

Postavi temu Odgovori

Srodne teme
Navigacija
Lista poslednjih: 16, 32, 64, 128 poruka.