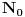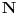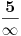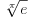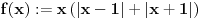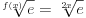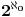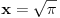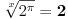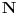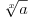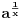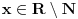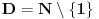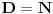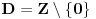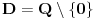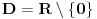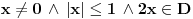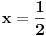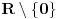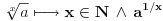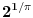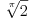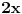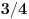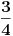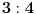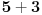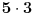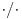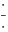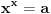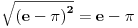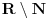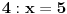@Bojan Basic:
Neke od ranijih verzija
Mathematica-e imale su interesantan bug: po njima je bilo
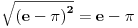
.
Da li iko može da garantuje da više nema takvih bisera? Svi znamo da je dokazivanje korektnosti programa veoma težak a u opštem slučaju zapravo i nerešiv problem. Na kraju, sve definicije su uneli ljudi (nešto ne verujem da u dubini radi neki cellular automata engine i usput otkriva matematičke zakone

) - pa se pitanje, dakle, svodi na to kojim ljudima verovati. Nadam se da ne misliš da je masovnost korisnika neka garancija kvaliteta proizvoda - jer je lako pronaći mnoštvo kontraprimera - npr. šta misliš, da li
chupcko sluša
Britney Spears 
?
Takođe, nadam se da ne može da te prevari
"efekat kineske sobe".
Da stvari nisu bile uvek kao danas (po pitanju indeksa korena) svedoči sledeće:
Citat:
The radical symbol:
By the close of the 17th century the symbolism was, therefore, becoming fairly well standardised, although there still remained some work to be done. The 18th century saw this accomplished, and it also saw the
negative and fractional exponent come more generally into use.
History of Mathematics volume II,
Smith, D.E., Dover Publications 1958
...naravno, samo pod uslovom da
Smith eksponentom zove ono što ja zovem indeksom

Pogledao sam malo i
Ojlerov Uvod u analizu beskonačno malih iz 1748. - čovek je vrlo dosledno upotrebljavao notaciju sa stepenima kad god bi imao posla sa eskponentima čija recipročna vrednost (ako postoji) pripada skupu
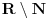
- mislim da je svima poznato koliki je bio uticaj te knjige...
@chupcko:
Citat:
chupcko: A iskreno celobrojno stepenovanje se lakse uvodi deci nego koren

sa ovim se, naravno, slažem - pa sad imam utisak da ti se u prethodnom postu
slučajno desilo da napišeš da se stepenovanje racionalnim brojevima radi pre uvođenja korena.
Što se tiče zvanične definicije korena (ili bilo kog mat. pojma) zaista ne postoji ništa tipa:
ISO Math 2006 
, ali zato možemo pogledati šta piše u zvaničnim udžbenicima najboljih mat. fakulteta širom planete - pa da vidimo do kakvih zaključaka dolazimo.
Ja ni malo ne brkam cifru kojom se broj nula označava sa samim pojmom nule. Zapravo imam jednu
nedovršenu raspravu sa
Nedeljkom na tu temu

. A uz to Arapi, recimo, označavaju broj 5 sa 0 (a broj 0 sa . )

Da li ti misliš da se može razumeti šta predstavljaju zapisi u kojima se javlja cifra nula a da se ne razume šta ta cifra označava? U mističkom smislu, za mene je 0=tao=celo, pa je 0 nekako sveobuhvatna i ako se to sme reći, najveća i nepromenljiva - otuda mi se valjda i sviđa šta je na tu temu mislio:
Citat:
John Wallis:
It is curious to note that Wallis rejected as absurd the now usual idea of a negative number as being less than nothing, but accepted the view that it is something
greater than infinity. Despite this he is generally credited as the originator of the idea of the number line where numbers are represented geometrically in a line with the positive numbers increasing to the right and negative numbers to the left.
Dakle, "koliko" treba dodati npr. konačnom broju 1 da bi se dobila takva beskonačna 0? Konačno ili beskonačno?

Sad se setih, postoji i jedna kratka priča
Majstori lože -
Ursule Legvin u zbirci
Dvanaest četvrti vetra u kojoj se opisuje otkriće (i simbolika) nule i negativnih celih.
Ursula je amater - pa ne očekujte bog zna šta...

Attempt all the problems. Those you can do, don't do. Do the ones you cannot.
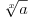 podrazumeva
podrazumeva 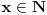 , dok zapis
, dok zapis 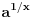 podrazumeva
podrazumeva 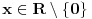 . Mene u zemlji Srbiji tako nikad nisu učili (nego me učili da su oba zapisa potpuno ekvivalentna, sem vizuelno) - je li čovek u pravu? Ili je to tako samo u Rumuniji i možda još nekoj zemlji? (Poznato mi je, recimo, da Rumuni i Bugari, mimo ostatka sveta, uključuju nulu u skup prirodnih brojeva.)
. Mene u zemlji Srbiji tako nikad nisu učili (nego me učili da su oba zapisa potpuno ekvivalentna, sem vizuelno) - je li čovek u pravu? Ili je to tako samo u Rumuniji i možda još nekoj zemlji? (Poznato mi je, recimo, da Rumuni i Bugari, mimo ostatka sveta, uključuju nulu u skup prirodnih brojeva.)



 Zbunio me čovek...
Zbunio me čovek...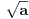
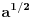
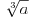
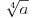
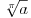
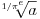
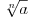
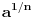
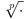
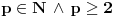
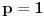
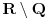
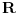
 Re: Zbunio me čovek...
Re: Zbunio me čovek... Re: Zbunio me čovek...
Re: Zbunio me čovek...