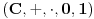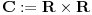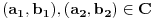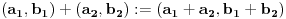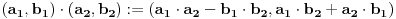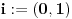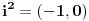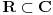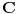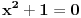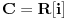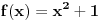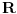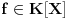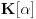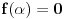Nije bas jednostavno odrediti da li "nesto" postoji ili ne. Ovakvu definiciju je dao Hilbert:
Kada nesto postoji?
Kada predpostavimo da postoji i to nas ne dovede do kontradikcije.
Znaci postupak je da pretpostavimo da "nesto" postoji i ako dobijemo kontradikciju znaci da ne postoji. Ako ne dobijemo kontradikciju dobili smo nesto lepo, neku novu teoriju. Tako valjda i nastaju sve konstrukcionisticke teorije.
Odatle je svojevremeno posao i Ojler:
Imamo polje R i jednacinu
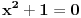
Pretpostarvimo da postoji njeno resenje i oznacimo ga sa

. Ispostavilo se da nismo dobili kontradikciju, dobili smo novu strukturu - polje kompleksnih brojeva
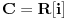
Zato se meni licno ne svidja ona definicija polja kompleksnih brojeva preko uredjenih parova, jer se ne vidi lepo motivacija za njihovo uvodjenje. Lepse je definisati polje kompleksnih brojeva kao korensko polje polinoma
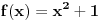
Ali dobro, to je samo stvar ukusa, i mozda potrebnog predznanja. Verovatno se u srednjim skolama ne moze pricati o korenskim poljima.
 takava broj da je
takava broj da je 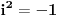 itd...
itd...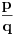 ,
, 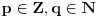




 def. kompleksnog broja
def. kompleksnog broja