Zadatak je iz predmeta Elementarna matematika.
Ne verujem da je dozvoljeno korišćenje uslovnih ekstrema.
Težak jeste.
Mislim da je nerešiv bez izvoda.
Lako se dokaže, preko nejednakosti sredina, da su tvrđenje i dati uslov ekvivalentni sa:
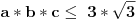
To jeste tačno, jer dati uslov daje garanciju
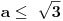
i
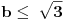
i
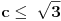
Pitanje je: "do kada je zbir veći od od proizvoda".
Ako su dva broja, onda do prvog korena(2).
Ako su tri broja, a ovde jesu tri broja, onda do drugog korena(3).
To zna svaki igrač kladionice, iole bolji od Konjislava.
Ali, to treba dokazati bez izvoda.
Ako bi bila 4 broja, onda do trećeg korena(4).
Ako bi bilo 5 brojeva, onda do četvrtog korena(5),...itd...
Ali da ne generalizujemo kada, bez izvoda, nema dokaza za ni za n jednako 3.
[Ovu poruku je menjao miki069 dana 16.06.2017. u 13:48 GMT+1]