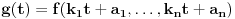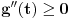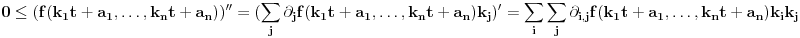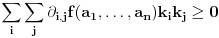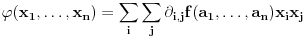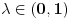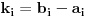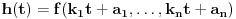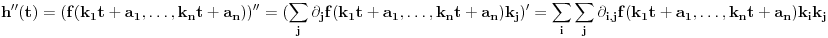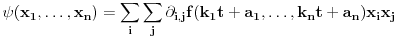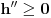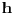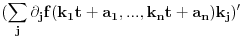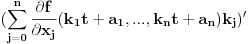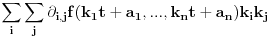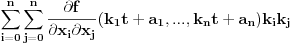• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 21.07.2003. uporedjivanje koda 15.12.2003. Statistička analiza Web log-a(proračun) - pose�.. 03.09.2004. upload problem ,postavim fajl al ga posle nema 12.02.2005. Nova matematicka analiza 18.05.2005. sendmail vs. postfix 04.12.2005. Literatura za oblasti:visestruki integrali, kompl.. 25.10.2010. ABC analiza u ERP sistemima 30.11.2006. Analiza poslovanja sa aspekta ekonomicnosti 04.01.2009. projekat sistema elektronskog poslovanja postojec.. 03.01.2007. projekat sistema elektronskog poslovanja postojec.. Navigacija Brisanje liste Aktuelne teme u ovom forumu: Još jedan zadatak sa uglovima Treći zadatak sa uglovima Ostala rešenja algebarske jednačine Lep zadatak sa uglovima Najmanje pozitivno realno r Ikosaedar i gustina ms matematika.... Jedan zadatak sa pravouglim trouglom Japanese | Can you solve this ? | Math.. Jednakostraničan trougao Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Zanimljiv zadatak o uglovima trougla Stado Boga Sunca ... 2000 godina star .. Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

uvelaruza Član broj: 315832 Poruke: 71 *.teol.net. +25 Profil Analiza zadatakkkkk 05.02.2014. u 13:52 - pre 136 meseci Da li bi mi neko mogao pomoći da riješim ovaj zadatak? Ne znam baš fino da to ovde otkucam, pa sam slikala... Može li mi neko pomoći? Hvala puno. [url=https://static.elitesecurity.org/uploads/3/4/3406447/mmmmmmmmmm.jpg] [Ovu poruku je menjao uvelaruza dana 07.02.2014. u 09:01 GMT+1] [Ovu poruku je menjao uvelaruza dana 07.02.2014. u 09:01 GMT+1] Follow your dreams, they know the way... Prikačeni fajlovi mmmmmmmmmm.jpg - 92.79k Odgovor na temu

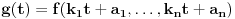
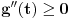
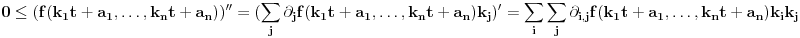
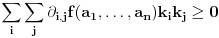
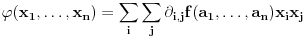
Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.ptt.rs. +2801 Profil Re: Analiza zadatakkkkk 05.02.2014. u 17:43 - pre 136 meseci Ako je konveksna, onda je svaka od funkcija konveksna, pa je , odnosno , odnosno . Drugim rečima, funkcija je pozitivno poludefinitna u tački , pa je na osnovu Silvesterovog kriterijuma, poyitivno poludefinitna Silvesterova matrica funkcije u tački , koja je jednaka Silvesterovoj matrici funkcije u tački . Pretpostavimo pozitivnu poludefinitnost Silvesterove matrice funkcije na oblasti . Izaberimo ma koje tačke i i ma koje . 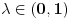Neka je . 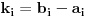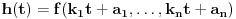Za funkciju važi . 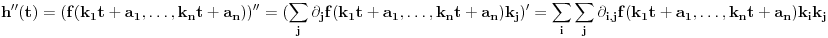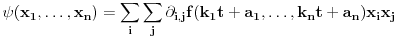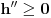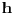Na osnovu Silvesterovog kriterijuma, za svako je funkcija pozitivno poludefinitna, pa je nenegativna, pa je , pa je funkcija konveksna, a samim tim i . Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

uvelaruza Član broj: 315832 Poruke: 71 *.teol.net. +25 Profil Re: Analiza zadatakkkkk 06.02.2014. u 11:27 - pre 136 meseci Hvala Vam puno. Samo da pitam za ovo što ste pisali .. Je li to u stvari ? I, ovo je li ? [Ovu poruku je menjao uvelaruza dana 06.02.2014. u 12:48 GMT+1] [Ovu poruku je menjao uvelaruza dana 06.02.2014. u 12:49 GMT+1] Follow your dreams, they know the way... Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.dynamic.isp.telekom.rs. +2801 Profil Re: Analiza zadatakkkkk 06.02.2014. u 11:52 - pre 136 meseci Da. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu