[es] - Problem sa zadarkom iz realne analize

pitagorina.teorema
Student, pmf
Kuba

Član broj: 307271
Poruke: 11
*.teol.net.

+10 Profil

Problem sa zadarkom iz realne analize

^{28.09.2012. u 10:42 - pre 153 meseci}

Potrebna mi je ideja za rješavanje zadatka lim (n → beskonačno) integral u granicama od 0 do pi (n na 3/2*x*sinnx)/(1+n na 2*x na 2)

Obicno u ovakvim zadacima za dominantu, tj g(x) uzimamo nulu prvog izvod niza posmatranog kao f-ja argumenta ne uvrstenu u fn(x), medjutim kad imam sin previse se zakomplikuje i ne mogu da dobijem nulu prvog izvoda.. :/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Problem sa zadarkom iz realne analize

^{28.09.2012. u 13:24 - pre 153 meseci}

Dakle, zanima te

.

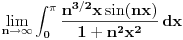
Jedno rešenje je da sinus oceniš jedinicom odozgore, tj. potražiš integralnu dominantu za niz funkcija

.

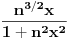
Ona će samim tim biti integralna dominanta tvog niza funkcija i iznosi

.

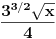
Drugo rešenje je da uvedeš smenu

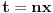
, posle čega imaš

.

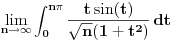
Označimo podintegralnu funkciju sa

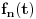
. Ako je

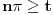
, onda je

.

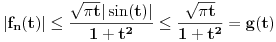
Ukoliko je pak

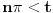
, onda je

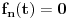
, pa svakako važi procena

.

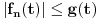
Dakle, integralna dominanta je

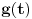
. Njena integrabilnost se lako dokazuje poredbenim kriterijumom (a moguće ju je integraliti tačno smenom

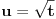
) ocenjivanjem jedinicom levo od jedinice, odnosno sa

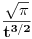
desno od jedinice.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

pitagorina.teorema
Student, pmf
Kuba

Član broj: 307271
Poruke: 11
*.teol.net.

+10 Profil

Re: Problem sa zadarkom iz realne analize

^{28.09.2012. u 18:20 - pre 153 meseci}

Hvala puno. Mene je bunilo ovo sinNX, dakle njega mogu ograničiti odozgo i onda posmatrati taj niz. Još jednom, hvala. :)

Odgovor na temu

pitagorina.teorema
Student, pmf
Kuba

Član broj: 307271
Poruke: 11
*.teol.net.

+10 Profil

Re: Problem sa zadarkom iz realne analize

^{28.09.2012. u 18:31 - pre 153 meseci}

Ja se izvinjavam, još samo ovo da pitam :$

\lim_{n\rightarrow\infty}\int_0^\infty}\frac{e^{1/x}\sin(ne^{-1/x})}{1+n^2}\,dx

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Problem sa zadarkom iz realne analize

^{28.09.2012. u 19:35 - pre 153 meseci}

Dakle, ovaj:

Integral pod limesom ne postoji ni za jedno

jer je

,

pa limes neodređeno divergira (dakle nije beskonačno ili nešto slično).

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

pitagorina.teorema
Student, pmf
Kuba

Član broj: 307271
Poruke: 11
*.teol.net.

+10 Profil

Re: Problem sa zadarkom iz realne analize

^{28.09.2012. u 20:46 - pre 153 meseci}

Mene zanima kako da nađem dominantnu f-ju g(x), kako da odredim od čega mi je manje ili jednako npr e na 1/x i sl. :/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Problem sa zadarkom iz realne analize

^{28.09.2012. u 22:34 - pre 153 meseci}

Pa, nećeš je naći. Matematika se ne radi napamet, niti na silu. Ako je dokazano da integral ne postoji, on ne postoji i gotovo.

Integral pod limesom je

Niz koji ima na beskonačno mnogo mesta

i na beskonačno mnogo mesta ima vrednost

nema limes.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Problem sa zadarkom iz realne analize

^{28.09.2012. u 22:43 - pre 153 meseci}

Evo ti ga još jedan zadatak:

Izračunati

.

Smenom

zadatak se svodi na

.

Ako bi postojala integralna dominanta, onda bi bilo

.

Pošto to nije tačno, jer je limes jednak 1, integralna dominanta ne postoji.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

pitagorina.teorema
Student, pmf
Kuba

Član broj: 307271
Poruke: 11
*.teol.net.

+10 Profil

Re: Problem sa zadarkom iz realne analize

^{29.09.2012. u 08:37 - pre 153 meseci}

Razumijem, samo po teoremi, limes mi ne smije ući pod integral ako ne postoji g(x) koja je veća ili jednaka od fn(x) i koja je integrabilna. :S
I da, šta kada u granicama integrala imam n, recimo

\lim_{n\rightarrow\infty}\int_n^\2n\frac{e^{-nx/n+1}\,dx

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Problem sa zadarkom iz realne analize

^{29.09.2012. u 09:19 - pre 153 meseci}

Jesi li na ovo mislio?

Ovo je isto što i

Integralna dominanta je

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Problem sa zadarkom iz realne analize

^{29.09.2012. u 10:15 - pre 153 meseci}

Mala pomoć oko (La)TeX-a za pitagoru:
\lim_{n\rightarrow\infty}\int_n^\2n\frac{e^{-nx/n+1}\,dx
Nije dobro napisano nekoliko stvari.

\2n ne postoji,treba staviti {2n}

\frac{e^{-nx/n+1} nevalja,treba \frac{brojnik}{nazivnik}

Da bi provjerio valja li formula pritisni dugme "Pogledaj kako odgovor izgleda".
Ako nešto nije ispravno vrati se na pisanje odgovora ("Go back one page") i popravljaj.
Kad središ da izgled valja "Pošalji odgovor"

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu