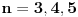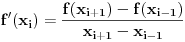Dobro, aj da pokusam nesto (
nisam testirao)
Code:
function [prvi drugi] = izvodi(X,Y,x)
n = length(X);
% pravimo tablicu konacnih razlika
kRazlike = zeros (n-1,n);
for i = 1:n-1
kRazlike (i,1) = Y (i+1)-Y (i);
end
for j = 2:n-1
for i = 1:n-j
kRazlike (i,j) = kRazlike (i+1,j-1) - kRazlike (i,j-1);
end
end
%prikazujemo ih korisniku
disp (kRazlike);
% I NJUTNOV INTERPOLACIONI POLINOM
% y = Y (1)+ q*kRazlike (1,1) + q*(q-1)*kRazlike (1,2)/2! + q*(q-1)*(q-2)*kRazlike (1,3)/3! + ...
%sta sad radim? napravicu polinom po q, i onda cu iskoristiti ugradjenu funkciju za diferenciranje polinoma
pol = [1 0] %ne znam koliko si upoznat sa ovakvim zapisom, ovo su koeficijenti polinoma,
%ovde je to polinom jedinicni q, da je pisalo [3 -2] bilo bi 3q-2
fakt = 1;
Njutn = [Y (1)];
for i = 1:n-1
fakt = fakt*i;
Njutn = [0 Njutn] + kRazlike (1,i)*q/fakt;
pol = conv (pol, [1 -i]); %funckija conv za mnozenje polinoma
end
h = X (2)-X (1);
q = (x-X (1))/h;
vrPol = polyval (Njutn,q) %funckija polyval racuna vrednost polinoma (prvi argument) u tacki (drugi argument),
% dakle mi ovde u stvari racunamo f(x), jer q zavisi od x, mi mu prosledimo x,
% on izracuna q (mi smo napravili polinom po q) i onda on vrati vrednost f(x)
prviIzvod = (polyder (Njutn))/h; %polyder vraca diferenciran polinom koji je zadatak kao argument, i delimo sa h,
% recimo po formuli da je tako (al objasnjenje za to je
% u stvari to da je d(Njutn)/d(x) = d(Njutn)/d(q) * d(q)/d(x), a d(q)/d(x) = 1/h)
vrednostPrvogIzvoda = polyval (prviIzvod,q) %i evo, izracunao si vrednost prvog izvoda u tacki x
%(ovde nisam stavio ; da bi mi stampao prvi izvod u toj tacki)
prvi = vrednostPrvogIzvoda; % ovo funkcija vraca
%drugi izvod? nikakav problem, samo iskoristis polinom za prvi izvod
drugiIzvod = (polyder(polyder (Njutn)))/(h*h); %ovo nisam siguran dal ce raditi (zbog dvostrukog poziva),
%mozes da izdvojis T = polyder(Njutn), pa da kazes polyder(T)...
vrednostDrugogIzvoda = polyval(drugiIzvod,q);
drugi = vrednostDrugogIzvoda;
% ako zelis da izracunas izvode i u cvornim tackama, onda mozes samo da napravis novi fajl,
% i tamo se pozoves na ovu funkciju, pustis jednu for petlju i to je to
Problem koji se javlja ako se radi drugacije, jeste da od toga koliko je

zavisi i to kakav ce nas polinom za f'(x) izgledati, jer se on i inace racuna peske, diferencira se clan po clan, ne postoji neka univerzalna formula za proizvoljno

(tacnije, mozda i postoji, ali meni nije poznata (sve vreme govorim o interpolacionom polinomu sa konacnim razlikama)). Mozes da napravis interpolacioni polinom za neko konkretno

, pozeljno malo, npr
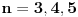
i onda se zadatak moze uraditi pesacki, samo prekucas gotove formule i to je to. Za neko malo vece

se stvari dosta komplikuju.
Vrednost prvog (drugog, svejedno) izvoda moze se naci mnogo lakse ako se koristi aproksimacija koja se dobija iz Tejlorovog razvoja funkcije, naime, vazi
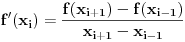
(slicno za drugi izvod), i onda na osnovu cvorova i vrednosti prvih izvoda u cvorovima ti mozes da napravis neki interpolacioni polinom i lako da nadjes vrednost prvog izvoda u nekoj tacki (za koju ima smisla posmatrati, da ne trazis u nekoj mnogo dalekoj tacki, jer onda dolazi do ekstrapolacije).
[Ovu poruku je menjao Sonec dana 25.05.2012. u 23:15 GMT+1]
Leonardo da Vinči
Nema istine u onim naukama u kojima se matematika ne primenjuje.
Milorad Stevanović
Bog postoji zato sto je matematika neprotivurečna.




 Matlab funkcija, potrebna pomoci
Matlab funkcija, potrebna pomoci