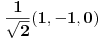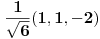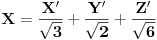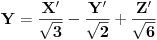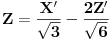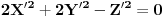Srodne teme

02.07.2002. Interbase, cudno pitanje
05.10.2004. Izjestaj... Pisanje slogova u dva reda na jednom ..
12.04.2005. Kako povezati razlicite prikljucke
27.04.2005. Hitno zadatak za sumu reda!!!!!!?
08.06.2005. Help!!! red elemenata...
29.08.2005. Teoreme Silova - naizgled standardan zadatak
12.03.2006. Ojlerove smene za svođenje integrala iracionalne..
22.03.2006. MsgBox - prikazivanje poruke u dva reda
13.05.2010. Kucanje teksta u dva reda u label-u
09.06.2007. [Firefox 2.0.0.1] tabovi u dva reda

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.

Površ drugog reda

[es] :: Matematika :: Površ drugog reda

[ Pregleda: 1778 | Odgovora: 2 ] > FB > Twit

Autor

miki069

Član broj: 161528
Poruke: 2056
212.200.34.*

+391 Profil

Površ drugog reda

^{05.01.2012. u 22:20 - pre 162 meseci}

Zadatak:
Jednačinu površi drugog reda: 6X^2 + 5Y^2 + 7Z^2 - 4XY - 4XZ + 36X - 36Y izomertijskom transformacijom svesti na kanonski oblik.
Uradim bez problema. Karakteristični polinom matrice kvadratne forme nema višestruke nule.

Međutim kad god se u primeru pojavi da karakteristični polinom matrice kvadratne forme ima višestruke nule, neće pa neće.
Kao primer X^2 + Y^2 + Z^2 - 2XY - 2XZ - 2YZ.

Ovek mi posle promene koordinata ostane neki mešoviti član.
Karakteristični vektori su dobro određeni i dijagonalazacija matrice kvadratne forme je moguća.

Gde grešim?

U literaturi koju imam nema ni jedan primer urađen sa višestrukim nulama.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Površ drugog reda

^{06.01.2012. u 11:09 - pre 162 meseci}

Kod određivanja sopstvenih vektora koji odgovaraju višestrukoj sopstvenoj vrednosti moraš voditi računa o tome da izabereš ortonormirane vektore i to je sve.

Dakle, u ovom primeru kod određivanja sopstvenih vektora pridruženih sopstvenoj vrednosti 2 prvo odrediš linearno mezavisne vektore (x,y,z) takve da je x+y+z=0, recimo (1,-1,0) i (1,0,-1), pa onda Gram-Šmitovim postupkom ortogonalizacije odrediš ortonormiran sistem sopstvenih vektora, kao što je