Ja sad pisem po nekom secanju, ali mislim da sam ovo dobio naucio jer je to bio jedan od najtezih ispita na faksu:
1. Slucajna promenljiva je preslikavanje skupa verovatnoce
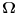
u skup realnih brojeva. Svakom ishodu

iz
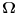
se dodeljuje neka realna vrednost
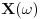
2. Funkcija raspodele slucajne promenljive X u nekoj tacki je definisana sledecim izrazom:
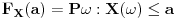 Osobine funkcije raspodele:
Osobine funkcije raspodele:
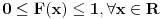
F je monotono neopadajuca funkcija
F je neprekidna sa desne strane u svakoj tacki
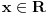
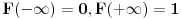
3. Neka je funkcija raspodele slucajne promenljive X glatka. Njen prvi izvod je funkcija gustine verovatnoce:
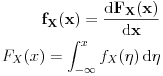 Osobine funkcije gustine verovatnoce:
Osobine funkcije gustine verovatnoce:
Vrednost funkcije gustine verovatnoce u nekoj tacki je srazmerna verovatnoci da slucajna promenljiva uzme vrednost iz okoline te tacke.
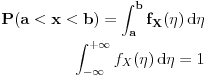
I da ne zaboravim
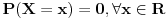
4. Matematicko ocekivanje
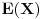
slucajne promenljive X sa funkcijom gustine raspodele

je dato izrazom:
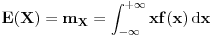
Varijansa predstavlja meru rasipanja slucajne promenljive oko srednje vrednosti i definise se kao
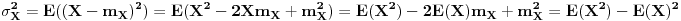
Za Normalnu (Gausovu) raspodelu imas i na wikipediji i to dosta toga. Bitno je da znas da je znacajna zbog posledica CGT (centralne granicne teoreme) koja kaze da raspodela sume nezavisnih slucajnih promenljivih sa istom raspodelom konvergira ka normalnoj raspodeli.
Dosta od mene, raspisao sam se i vise nego sto je trebalo.