[es] - Problem s eksponentima

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dynamic.sbb.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Problem s eksponentima

^{21.06.2010. u 17:46 - pre 180 meseci}

Holononi, ti, izgleda, ne znaš značenje pojma dokaz. To što Cabo eventualno ne može da nađe tačku za koju tvoj argument pada i dalje ne znači da ti je argument matematički ispravan. Evo ilustracije.

Problem:

Ispitati da li za

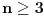
u skupu

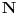
postoji rešenje jednačine

.

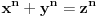
Moje „rešenje“:

Data jednačina ekvivalentna je sa

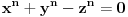
. Kada je zapišemo u ovom obliku, odmah vidimo da nema rešenja.

Cabo prigovara:

Čekaj, ne slažem se da se iz tvog oblika odmah vidi da jednačina nema rešenja. Dokaži i taj deo.

Ja odgovaram:

Ako jednačina u mom obliku ima rešenje, tada postoji tačka

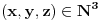
za koju je ispunjeno

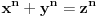
. Ne bilo ti teško, navedi tu tačku.

Da li sad vidiš koliko ti je argumentacija šuplja? Matematika se ni u ludilu tako ne radi. Ali OK, ako bi i dalje terao po svome, evo konačnog udarca.

Citat:

Farenhajt:
Ako su

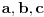
pozitivni realni brojevi, ispitati da li važi

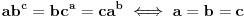
Dokazaćemo da ekvivalencija iz postavke ne važi. Uzmimo

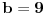
. Da bismo zadovoljili uslov

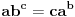
, možemo birati

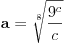
(direktno se proverava). Dakle, dovoljno je još pokazati da postoji

takvo da važi

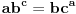
, tj.

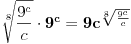
. Posmatrajmo funkciju

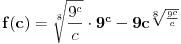
. Ova funkcija očito je neprekidna za

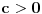
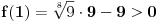
. Dalje, važi

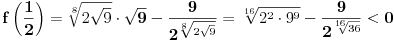
(poslednja nejednakost može se proveriti uz malo dosadnog, „pipavog“, ali ne previše teškog računa). Dakle, postoji

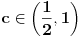
za koje važi

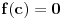
, što je i trebalo dokazati.

Približne vrednosti:

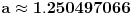
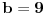
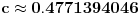
Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Problem s eksponentima

^{21.06.2010. u 18:01 - pre 180 meseci}

Hvala na savetu ali moram da primetim da to što pišeš nema veze sa zadatkom. I ne znam zašto razvodnjavaš temu. Obriši višak posta da ne skrećemo sa teme. Naivno je smatrati da ja ne znam šta je dokaz. Ja ovde ne polažem nikome račune. Ko ima bolji dokaz neka ga iznese.

Elementarno je da linearna, stepena i eksponencijalna funkcija imaju različite priraštaje za istu promenu argumenta. Ja sam iz toga izveo zaključak kako sam izveo. Ako neko ima drukčiji dokaz neka ga iznese. Isto tako možete pobijati stav o priraštajima od koga sam krenuo ali ne možete reći "nije dokaz" jer taj "nedokaz" niste oborili pukom tvrdnjom "nije dokaz".

Odgovor na temu

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Problem s eksponentima

^{21.06.2010. u 18:44 - pre 180 meseci}

I još nešto. Kako si došao do toga da je c~0.48 i c iz intervala (1/2, 1)?

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dynamic.sbb.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Problem s eksponentima

^{21.06.2010. u 19:19 - pre 180 meseci}

Citat:

holononi:
Hvala na savetu ali moram da primetim da to što pišeš nema veze sa zadatkom.

Nema veze sa zadatkom, ali ima veze s onim tvojim tekstom za koji tvrdiš da predstavlja dokaz tvrđenja zadatka. Ako je ono tvoje stvarno dokaz dotičnog tvrđenja, onda je ono moje dokaz velike Fermaove teoreme.

Citat:

holononi:
Ko ima bolji dokaz neka ga iznese.

Nije se tražio bolji dokaz, tražio se korektan dokaz. Tvoj nije, pa se ne ubraja u dokaze. U međuvremenu sam ponudio kontraprimer, pa je postalo jasno da dokaz tvrđenja kojim si se ti bavio i ne postoji. No, ta „sitnica“, činjenica da tvrđenje koje pokušavaš dokazati nije tačno, tebe ne sprečava da i dalje tvrdiš kako je tvoj „dokaz“ korektan — neverovatno! Jesi li uopšte svestan šta govoriš? Vraćamo se na početak moje prošle poruke — očito ne znaš značenje pojma dokaz.

Citat:

holononi:
Elementarno je da linearna, stepena i eksponencijalna funkcija imaju različite priraštaje za istu promenu argumenta.

Nije tačno (bar ne tako kako si ti zamislio). Evo,

(linearna funkcija) i

(stepena funkcija). Posmatrajmo tačku

(u njoj važi

) i priraštaj

. Tada imamo

, pa važi

. Šta ćemo sad?

Citat:

holononi:
ne možete reći "nije dokaz" jer taj "nedokaz" niste oborili pukom tvrdnjom "nije dokaz".

OK. Nije dokaz zato što nije svaki korak matematički utemeljen. Je l’ sad u redu?

Citat:

holononi:
Kako si došao do toga da je c~0.48 i c iz intervala (1/2, 1)?

Loš primer, zahvaljujem na primedbi. Primer koji bi odgovarao rešenju koje sam napisao jeste

. (Naravno, ove približne vrednosti same po sebi ne znače mnogo, suština je u priči koja je prethodila. Približne vrednosti su tu samo radi lakšeg poimanja.)

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Problem s eksponentima

^{21.06.2010. u 21:04 - pre 180 meseci}

Problem je što vi u svojim diskusijama proizvoljno prišivate ljudima šta hoćete. Ovde
http://www.elitesecurity.org/t402777-0#2629759
sam izneo procenu a ne spominje se "dokaz". Drugi su tražili dokaz ali su za sebe zadržavali pravo da diskutuju bez dokaza. Zašto bih ja bio uskraćen za to pravo?

Tako i ti izmišljaš da sam ja tvrdio da je "moj dokaz korektan". Ja samo pišem šta sam razmišljao a nisam tvrdio da sam dokazao.

Pronadji "onaj moj tekst" u kome "tvrdim da predstavlja dokaz tvrđenja zadatka"

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
212.200.65.*

+2801 Profil

Re: Problem s eksponentima

^{21.06.2010. u 22:05 - pre 180 meseci}

Iz onoga što si pisao se jasno vidi da si to navodio kao rešenje. Ja sam se sa svojim "rešenjem" jasno ogradio od toga da je to konačno rešenje time da tu treba još nešto da se dokaže. Diskusija je nešto sasvim drugo od navođenja kao dokaza nečega što nije dokaz.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Problem s eksponentima

^{22.06.2010. u 08:49 - pre 180 meseci}

Šta vi imate meni da dokazujete?
Nisam ja postavio zadatak.
Nisam ja tvrdio da Nedeljkovo rešenje (koje takodje nije rešenje) nevalja.
Nisam ja bilo kome osporio bilo šta.
Jednostavno sam ispisao svoju procenu bez mlaćenja prazne slame po bilo kome.
Ko je imao rešenje mogao je da ga ispiše baš kao što sam i ja ispisao ne pominjući nikoga. Naravno, to ne znači da niko ne sme da se osvrće na moje komentare i da ih osporava. Svakako da može jer i ja volim da čujem kritiku mog rada ali u meri i način koja odslikava uljudno ponašanje.

Ovako, rešavanje zadatka je postalo sredstvo za nekulturno etiketiranje. Svi su imali priliku da reše zadatak ali umesto da reše zadatak (što je cilj foruma) neki su se pretvorili u pse lutalice.

Uzgred, osim neobaveznog ćaskanja i "filozofiranja" upuštanje u detaljnije rešavanje zadatka je uvek sumnjivo i ne odražava preteranu inteligenciju. Motiv da se tako nešto radi besplatno je pre svega nedostatak ličnosti kao što je i etiketiranje odraz nedostatka ličnosti. Zato i pokušaj da se nekom dokaže bilo šta što nije pitao nije ništa drugo nego nedostatak ličnosti. Takvi neka se istresaju na nekom drugom moliću lepo.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.isp.telekom.rs.

+2801 Profil

Re: Problem s eksponentima

^{22.06.2010. u 09:28 - pre 180 meseci}

Napisao si nešto što nije rešenje, navodeći da je kompletno rešenje. Čak si i pitao "šta tu treba da se dokazuje". Na kraju, kada se ispostavilo da nisi u pravu, očigledno si imao problem sa suočavanjem sa tom činjenicom (što bi neki rekli, nedostatak ličnosti) i zato nastavljaš sa ovakvim glupostima. DEa si napisao "uh, da zeznuo sam se" ili da ništa nisi napisao, to bi bila sasvim druga stvar. Ovako, osporavanje tvog rešenja ispada (po tvome) kao napad na tvoju ličnost.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Problem s eksponentima

^{22.06.2010. u 09:34 - pre 180 meseci}

Sad si i ti počeo da izmišljaš. Gde sam ja naveo "da je kompletno rešenje"? Da možda ne "praviš dimnu zavesu"?

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.isp.telekom.rs.

+2801 Profil

Re: Problem s eksponentima

^{22.06.2010. u 11:27 - pre 180 meseci}

Celo vreme si u tom fazonu. No, ovde se niko nije bavio tobom lično, već rešenjem koje si ponudio, čemu valjda forum i služi.

OK, zeznuli smo se obojica (jer se zadatak nije mogao rešiti ni mojim pristupom), ali nemoj zbog toga da se blamiraš.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Problem s eksponentima

^{22.06.2010. u 12:57 - pre 180 meseci}

Niko se ne bavi osim tebe i ostalih.
Kako sam primetio da tvoje rešenje nije uredno ja sam izneo procenu a da pritome nisam pljuvao ni po tebi ni po bilo kome drugom. Problem je što vi rešavate zadatak meni a ne onome ko je postavio zadatak. Nema razloga da meni neko bilo šta objašnjava osim ako time taj neko ne leči svoje frustracije. A ja naplaćujem lečenje fustracija.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.isp.telekom.rs.

+2801 Profil

Re: Problem s eksponentima

^{22.06.2010. u 13:23 - pre 180 meseci}

Niko nije pljuvao po tebi. Druga je stvar što kritiku tvog rešenja ti doživljavaš lično. Naravfno da je iz priloženog jasno da smatraš da si najpametniji i da tebi nema ko šta da objašnjava, ali forum služi za diskusiju onih koji žele da učestvuju, dok ostali ne moraju ni da se javljaju. Takođe, postavljaču teme je potrebno ukazati da neko od ponuđenih rešenja nije dobro.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

holononi

Član broj: 163572
Poruke: 658
*.adsl.verat.net.

+5 Profil

Re: Problem s eksponentima

^{22.06.2010. u 13:37 - pre 180 meseci}

A da tu smo, "smatraš da si najpametniji". Obrati se nekom psihologu i on će ti objasniti da ti ne možeš znati šta ja smatram ali možeš projektovati svoje "smatranje".

Sve smo objasnili, što se mene tiče tema može u arhivu. Hvala na strpljenju i nemojte zameriti.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.isp.telekom.rs.

+2801 Profil

Re: Problem s eksponentima

^{22.06.2010. u 13:41 - pre 180 meseci}

Citat:

holononi: Obrati se nekom psihologu i on će ti objasniti da ti ne možeš znati šta ja smatram ali možeš projektovati svoje "smatranje".

Da, niko ne može da pronikne u dubinu ove veleumne rečenice:

Citat:

holononi: Nema razloga da meni neko bilo šta objašnjava

Pametnije bi ti bilo da prestaneš da se blamiraš.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Mali Misha
Mihajlo Anđelković
NBGD

Član broj: 79396
Poruke: 379
92.244.144.*

ICQ: 195487525
Sajt: cpptea.com

+1 Profil

Re: Problem s eksponentima

^{22.06.2010. u 13:46 - pre 180 meseci}

holononi, čim ti neko kaže da ti je "argumentacija šuplja" i u sledećoj rečenici spomene ludilo, jasno ti je da razgovaraš sa ljudima koji ne biraju mnogo reči.

To i jeste problem, što se od pogrešnog/nepotpunog rešenja pravi velika dževa i prelazi se granica pristojnosti, umesto da se elegantno spusti pod tepih i produži dalje. A da vidiš kako samo isti ti divljaju i brane se do poslednjeg kada se pokaže da je nešto (što su oni radili ili branili) nepotpuno. Zaključavaju teme i brišu poruke koje njihove nebuloze nazivaju pravim imenom.

Ipak se ++uje.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.isp.telekom.rs.

+2801 Profil

Re: Problem s eksponentima

^{22.06.2010. u 13:59 - pre 180 meseci}

O ličnim osobinama (inteligenciji, nedostatku ličnosti, frustriranosti itd.) je upravo raspravljao holononi i niko drugi. Ko je ovde pomenuo ludilo?

Ja nisam moderator, pa ne mogu ni da brišem tuđe poruke, ni d azaključavam teme. Bojan mi je rekao da je tvoju poruku obrisao jer si prešao na lični plan, mada sam mu ja napomenuo da u toj poruci nisam našao ništa uvredljivo (jer mi je poruka stigla na meil pre nego što je obrisana). A što se tiče tvoje argumentacije o potpunosti rešenja, lično si ti izbegao da odgovoriš na postavljena pitanja i nastavio sa "argumentacijom" u stilu "Ja sam ovde profesor i tako je kako ja kažem".

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Cabo
Lokanje u bircuzu

Član broj: 10942
Poruke: 684
*.rcub.bg.ac.rs.

+5 Profil

Re: Problem s eksponentima

^{22.06.2010. u 15:20 - pre 180 meseci}

LOL, kao mala deca ste.