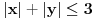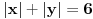Algoritam koji sam koristio pri rešavanju zadatka koji ću uskoro da navedem je sledeći:
1) Odredim Silvesterovim kriterijumom kandidate za lokalni bezuslovni ekstrem. U obzir uzimam samo one koji su unutar skupa K.
2) Odredim kandidate za uslovni ekstrem po svakom od m uslova posebno (granica skupa K). U obzir dolaze samo one tačke koje leže na granici skupa.
3) Sve tačke nediferencijabilnosti funkcije granice (preseci gr. f-je) su kandidati.
4) U svim tačkama iz 1), 2), 3) odredim vrednost funkcije i izračunam min i max.
Zadatak:
Izračunati min i max f-je na prethodni način:
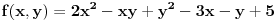
na skupu:
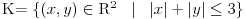
Rezultati:
1) A(1,1), f(A)=3
2) Koristio sam Lagrange-a: C(-7/8 , -17/8) , f(C) ~ 14, D(11/8, 13/8), f(D) ~ 3.5
3) Tačke nediferencijabilnosti su (3,3) => f=11 , (-3,3) => f=47 , (3,-3) => f=35 , (-3,-3) => f=35.
Nisam ispitivao prirodu tačaka, nego sam na kraju izabrao najmanju i najveću vrednost funkcije, dakle min f = 3 (to je tačno) , max f = 47 (netačno, tačan odgovor je 32)
Kako ?




 Određivanje globalnog min i max neprekidne funkcije na kompaktnom skupu
Određivanje globalnog min i max neprekidne funkcije na kompaktnom skupu