• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 21.01.2004. Zadatak sa opstinskog takmicenja 28.02.2005. Jedan zadatak sa olimpijade 22.11.2005. Lep zadatak ....... 02.12.2009. ...zadatak...pascal... 22.01.2006. [Zadatak]: Glasi: 21.03.2006. jedan zadatak sa saveznog 25.02.2008. zadatak iz otpornosti 11.11.2006. Jos jedan zadatak iz C-a! 29.05.2007. Kako da resim ovaj zadatak(hitno)!!! 14.02.2010. skolski zadatak,upomoc!!! Navigacija Brisanje liste Aktuelne teme u ovom forumu: Još jedan zadatak sa uglovima Treći zadatak sa uglovima Ostala rešenja algebarske jednačine Lep zadatak sa uglovima Najmanje pozitivno realno r Ikosaedar i gustina ms matematika.... Jedan zadatak sa pravouglim trouglom Japanese | Can you solve this ? | Math.. Jednakostraničan trougao Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Zanimljiv zadatak o uglovima trougla Stado Boga Sunca ... 2000 godina star .. Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

number22 Bez Član broj: 246412 Poruke: 44 *.opera-mini.net. +1 Profil Zadatak sa matricom i submatricom 16.01.2010. u 10:37 - pre 185 meseci Data je matrica formata 10x10 koja sadrzi tacno 15 elemenata jednakih nuli. Dokazati da postoji submatrica formata 5x5 koja ne sadrzi ni jednu nulu. Probao sam raznim rasporedom nula i uvijek postoji bar jedna submatrica 5x5 bez nule. Ali ne znam kako da dokazem to... Odgovor na temu

Cabo Lokanje u bircuzu Član broj: 10942 Poruke: 684 *.vdial.verat.net. +5 Profil Re: Zadatak sa matricom i submatricom 16.01.2010. u 15:22 - pre 185 meseci Kreni od suprotne pretpostavke, da ne postoji takva podmatrica, tj. da svaka podmatrica formata mora da sadrži bar jednu nulu, pa onda vidi koliko takvih može da se smesti u matricu formata . Kliknite da vidite kako da pišete matematičke formule u [tex]TeX[/tex]-u bez slanja slika Odgovor na temu

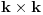
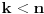
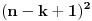
Cabo Lokanje u bircuzu Član broj: 10942 Poruke: 684 *.vdial.verat.net. +5 Profil Re: Zadatak sa matricom i submatricom 17.01.2010. u 16:34 - pre 185 meseci Ako se još nisi dosetio, evo ideje dokaza: Neka je podmatrica formata (). Tada postoji mogućih pozicija podmatrice u okviru „velike“ matrice. 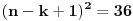Ako pretpostavimo suprotno, da svaka podmatrica mora da sadrži bar jednu nulu, i uzmemo najbolji mogući slučaj, da svaka sadrži tačno jednu nulu, krenuvši od gornjeg levog elementa matrice, brzo ćemo „istrošiti“ tih 15 nula, jer nam treba bar da bismo svakoj matrici pridružili „njenu“ nulu. Dakle, to je kontradikcija, pa postoji podmatrica koja ne sadrži nijednu nulu. Kliknite da vidite kako da pišete matematičke formule u [tex]TeX[/tex]-u bez slanja slika Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.ptt.rs. +2801 Profil Re: Zadatak sa matricom i submatricom 17.01.2010. u 18:23 - pre 185 meseci Ista nula može pripadati raznim matricama. Neće to biti sve različite nule. Drugačije to ide. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 212.200.65.* +2801 Profil Re: Zadatak sa matricom i submatricom 17.01.2010. u 23:30 - pre 185 meseci Uradiću po slučajevima. Ako postoji 5 vrsta sa po najviše jednom nenula komponentom, izbaci preostalih 5 vrsta i one kolone koje sadrže nenule u tih 5 vrsta. U suprotnom imaš bar 6 vrsta sa po bar dve nenule. Dakle, u preostale 4 vrste imaš najviše 3 nenule. Izaberi te 4 vrste još jednu od preostalih 6 vsta. Izbaci sve kolone koje u izabranim vrstama imaju nenulu. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

number22 Bez Član broj: 246412 Poruke: 44 *.opera-mini.net. +1 Profil Re: Zadatak sa matricom i submatricom 18.01.2010. u 15:22 - pre 185 meseci Evo do kakvog sam rjesenja dosao. Pocetnoj matrici formata 10x10 treba da se precrta (izbaci) 5 vrsta koje imaju najvise nula. Ako dve ili vise vrsta imaju jednak br. nula izbacujemo nasumicno jer nije bitno koja ostaje. Sada precrtamo svaku kolonu koja sadrzi nulu a koja nije prethodno precrtana. I na kraju ostaje trazena podmatrica koja je formata najmanje 5x5 a najvise 5x10 Hvala na pomoci Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 212.200.65.* +2801 Profil Re: Zadatak sa matricom i submatricom 18.01.2010. u 16:57 - pre 185 meseci To rešenje se poklapa sa mojim, s tim što sam dao i dokaz da ostaje najmanje 5 kolona. OK, i sam si došao do ispravnog rešenja. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu