|
miki069
Član broj: 161528
Poruke: 2056
212.62.55.*
|
Mozes i nekom numerickom metodom za nalazenje pribliznih resenja jednacine f(x) = 0.
- metoda polovljenja intervala,
- metoda secice ili
- metoda tangente.
za x=0 imas egzaktno resenje f(x) =0.
za x=1, x=2, x=3 i x=4 je funkcija negativna. Za x=5 je pozitivna. Resenje je negde na intervalu (4,5).
Metoda polovljenja intervala ne trazi formule i najjednostavnija je, ali i najsporija:
Resenje je negde na intervalu (4,5). Srediste intervala je 4.5
f(4.5)<0 => da je resenje x u intervalu (4.5, 5). Srediste je 4.75.
f(4.75)<0 => da je resenje u intervalu (4.75, 5). Srediste je 4.875.
f(4.875)<0 => resenje je u intervalu (4.875, 5) Srediste je 4.9375
f(4.9375)<0 => resenje je u intervalu (4.9375,5) Srediste je 4.96875
f(4.96875)>0 => resenje je u intervalu (4.9375, 4.96875) Srediste je 4.953125
f(4.953125)<0 => resenje je u intervalu (4.953125, 4.96875) Srediste je 4.9609375
f(4.9609375)<0 => resenje je u intervalu (4.9609375, 4.96875) Srediste je 4.96484375
f(4.96484375)<0 => resenje je u intervalu (4.96484375, 4.96875) Srediste intervala je 4.966796875
f(4.966796875)>0 => resenje je u intervalu (4.96484375, 4.966796875) Srediste intervala je 4.965820313
f(4.965820313)>0 => resenje je u intervalu (4.96484375, 4.965820313) Srediste intervala je 4.965332031
f(4.965332031)>0 => resenje je u intervalu (4.96484375, 4.965332031) Srediste intervala je 4.965087891
f(4.965087891)>0 => resenje je u intervalu (4.96484375, 4.965087891) Srediste intervala je 4.96496582
f(4.96496582)<0 => resenje je u intervalu (4.96496582, 4.965087891) Srediste intervala je 4.965026855
f(4.965026855)<0 => resenje je u intervalu (4.965026855, 4.965087891)
Ako je bila trazena tacnost od 0.001 => priblizno resenje x=4.9650
[Ovu poruku je menjao miki069 dana 18.06.2008. u 08:01 GMT+1]
|
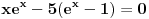
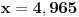
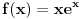 i
i 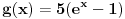 . Postoji li nacin bez crtanja funkcija?
. Postoji li nacin bez crtanja funkcija?