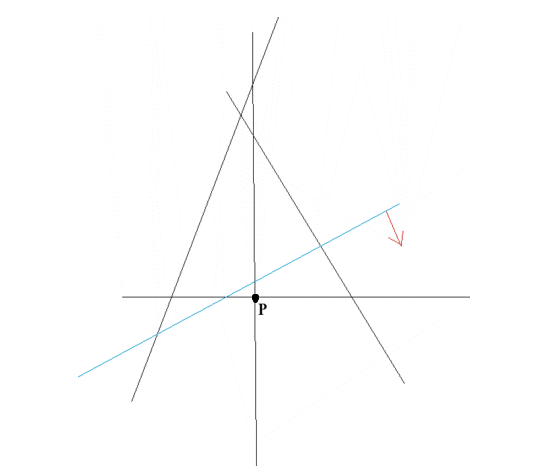
Ovaj dokaz koji je neor dao nikako nije ispravan, jer osim slučaja koji je gpreda spomenuo "gubljenje" trouglova može da se dogodi i na drugi način, na primer kao na slici (obratite pažnju šta se dešava kad prava obeležena plavom bojom pređe preko tačke P).
"Zvanični" dokaz, ako se ne varam, se svodi na to da svakoj pravoj pridružimo brzinu na takav način da kad prave počnu da se "kreću" površine trouglova koje one obrazuju ostaju konstantne, ali nažalost ne znam više detalja o ovakvom rešenju (ujedno bih zamolio da ako neko zna napiše tačno kako to ide). Ono što ću sada pokušati da prezentujem je jedan drugačiji dokaz, ako neko eventualno nađe grešku u njemu neka slobodno to napiše, ja mislim da je korektan.
Posmatrajmo proizvoljnu duž iz date podele i neka su njeni krajevi tačke

i

. Ta duž je zajednička za dve oblasti (od kojih jedna može biti i beskonačna). Posmatrajmo jednu od te dve oblasti. Neka je u njoj
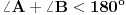
. U tom slučaju "stranu" duži koja se nalazi unutar te oblasti obojimo crveno, u suprotnom plavo (analogija bi bila recimo sledeća: neka su pomenute oblasti "sobe" a duži "zidovi", tako da bojimo onu stranu zida koja se nalazi u posmatranoj sobi). Istu uradimo i za drugu oblast koja sadrži tu duž, i ceo postupak ponovimo za sve duži. Očigledno je da sada svaka duž ima jednu crvenu i jednu plavu stranu (jer ukoliko je
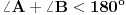
za jednu figuru neke duži onda za drugu figuru te duži zbir uglova u tačkama

i

iznosi
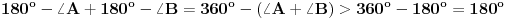
), pa je broj duži upravo jednak broju crveno obojenih strana. Takođe se lako zapaža da su u svakom trouglu sve tri strane njegovih duži obojene crveno. Posmatrajmo neku figuru iz date podele koja ima 4 ili više ivica. Dokazaćemo da ako u toj figuri postoje neke dve crvene duži u tom slučaju one moraju biti susedne. Pretpostavimo suprotno - neka su u figuri
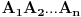
duži
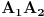
i
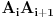
obojene crvenom bojom, za ostale nije bitno kako. Tada je
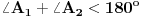
i
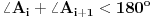
, odnosno
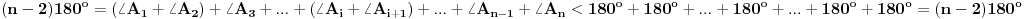
što je očigledna kontradikcija. Iz ovoga neposredno sledi da je u svakoj figuri sa 4 ili više stranica najviše 2 duži obojeno crvenom bojom. Neka je

ukupan broj duži i

ukupan broj konačnih figura u datoj oblasti. Ako sa

obeležimo broj trouglova u datoj podeli prebrojavanjem crvenih strana (podsetimo se da je njihov broj jednak broju duži) dobijamo:
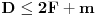
Znajući da je
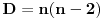
i
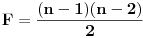
(obe stvari su poznate iz kombinatorike, prva je očigledna a druga se lako dokazuje indukcijom) uvrštavanjem ovoga u poslednju formulu imamo:
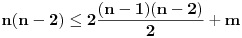
, odnosno
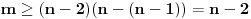
, što je i trebalo dokazati.
Ljubičice crvena, što si plava kô zelena trava.