Neka prirodan broj

ima dekadni zapis

. To znači da je
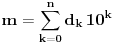
.
Po modulu 11 to izgleda ovako:
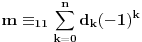
jer je
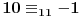
.
Stoga je
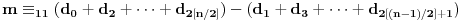
,
gde je
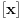
ceo deo od

.
Primera radi,
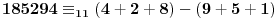
.
Drugim rečima, ako ciframa na parnom mestu nazovemo cifre uz stepen broja 10 na paran broj (cifre jedinica, stotina itd.), a ciframa na neparnom mestu cifre uz 10 na neparan broj (cifre desetica, hiljada itd.), onda razlika zbira cifara na parnim mestima i zbira cifara na neparnim mestima ima isti ostatak pri delenju sa 11 kao broj čiji je to zapis.
Odatle sledi da je broj deljiv sa 11 akko je pomenuta razlika deljiva sa 11. To je poznat kriterijum deljivosti sa 11. Konkretno, kod palindroma sa parnim brojem cifara ti zbirovi su jednaki, pa im je razlika 0, što je svakako deljivo sa 11.
Na sličan način se može formulisati kriterijum deljivosti sa 7.
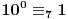
,
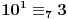
,
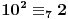
,
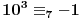
,
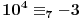
,
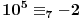
,
Obzirom da je
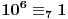
, za svako
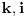
je
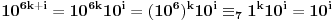
, tj. ovaj niz se periodično ponavlja, pa je
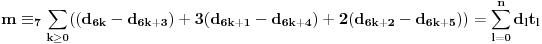
,
gde je
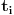
ostatak pri delenju
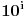
sa 7, što je periodičan niz sa periodom 6.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
 decimala broja
decimala broja 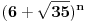 devetke?
devetke?