Postoji teorema koja kaze da broj nenegativnih resenja jednacine
(gde su
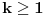
i
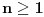
) iznosi
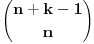
. Dokaz ovog tvrdjenja mozete naci
OVDE, strana 111. (ne mora bas preko ove teoreme, moze i preko posmatranja varijacija odredjenog tipa)
I mislim da je sad jasno zasto je
.
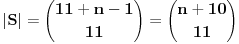
Dalje, mislim da je jasno zasto posmatramo jednacinu
. E sad, koja nama ovde resenja ne valjaju? Pa, ako je prva cifra nula, onda nam to resenje ne valja, jer onda to nije n-tocifreni broj, vec n-1-tocifren (il cak i manje, ako imas jos takvih nula). Da bi nasli koliko je takvih resenja, msm da je jasno da se to svodi na odredjivanje koliko jednacina
ima resenja. Takodje, nama su
jednocifreni brojevi, tako da nam ne odgovaraju ni resenja u kojima je za neko
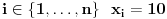
, odnosno
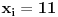
. Dakle, od svih resenja, oduzecemo uniju ovakvih resenja (koja nam ne valjaju), i primeniti princip ukljucenja-iskljucenja. Ako je
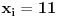
, onda su ostali clanovi jednaki nuli (dakle, jedinstveno su odredjeni), tako da nam ostaje samo da kazemo da imamo
nacina kako cemo da dodelimo vrednost 11 nekom
. Slicno za slucaj ako je
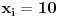
(za neko
), onda je jos jedan broj jednak jedinici, a ostali su nuli. Dakle, imamo n mogucnosti za to kome cemo da dodelimo 10 (ili 1, svejedno je), a zatim za n-1 broj odredjujemo kome cemo da dodelimo 1, dakle, ukupno
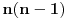
. Za formulu ukljucenja-iskljucenja nam trebaju i neki preseci, al to mozes i sam da vidis zbog cega je njihova kardinalost tolika (koliko je napisano).
Leonardo da Vinči
Nema istine u onim naukama u kojima se matematika ne primenjuje.
Milorad Stevanović
Bog postoji zato sto je matematika neprotivurečna.
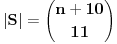Re: Dva pitanja, jedno bez ideje :( (SUMA)
?
ali hvala za hint
