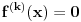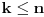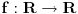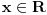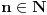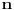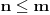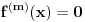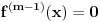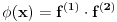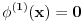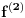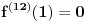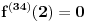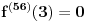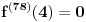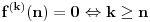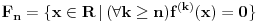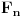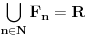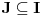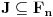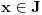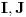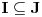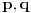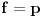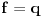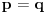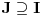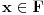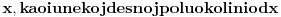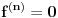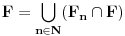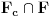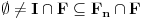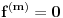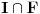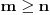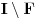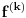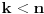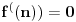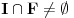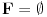Evo malo kraćeg rešenja.
Neka je
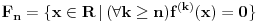
Očigledno je za svako

skup
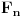
zatvoren. Takođe,
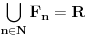
. Iz Berove teoreme o kategorijama sledi da za svaki neprazan otvoren interval

postoje

i neprazan interval
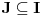
takvi da je
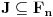
. Pošto je
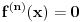
za sve
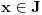
, funkcija

je polinom stepena ne većeg od

na skupu

.
Neka su
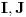
ma koji neprazni otvoreni intervali takvi da je
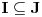
i neka su
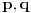
ma koji polinomi i neka je
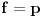
na skupu

i
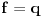
na skupu

. U tom slučaju, polinomi

i

se poklapaju na intervalu

, odnosno na beskonačnom skupu tačaka. Polinomi koji su jednaki u beskonačno mnogo tačaka se poklapaju, pa važi
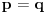
.
Neka je

ma koji interval na kome je funkcija

polinomijalna i neka je

polinom takav da je
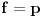
na

. Na ma kom intervalu
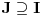
na kome je funkcija

polinomijalna važi
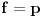
, pa je
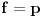
na uniji svih intervala koji sadrže interval

i na kojima je funkcija polinomijalna. Stoga je svaki otvoren interval na kome je funkcija

polinomijalna sadržan u nekom maksimalnom otvorenom intervalu na kome je funkcija polinomijalna.
Različiti maksimalni intervali na kojima je funkcija polinomijalna ne mogu se preklapati jer bi presek ta dva intervala bio interval na kome je funkcija

polinomijalna, pa bi bila jednaka istom polinomu na oba ta maksimalna intervala, kao i na njihovom preseku, odnosno bila bi polinomijalna na uniji ta dva maskimalna intervala suprotno njihovoj maksimalnosti.
Neka je

komplement unije svih maksimalnih otvorenih intervala na kojima je funkcija

polinomijalna. Očigledno je zatvoren.
Skup

nema izolovanih tačaka. U suprotnom, postojalo bi neko
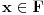
takvo da je

polinomijalna u bar nekoj levo poluokolini od
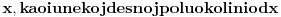
. Postojalo bi neko

takvo da je
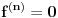
na nekoj okolini od

suprotno uslovu maksimalnosti intervala sa svake strane od

.
Ako je skup

neprazan, on kao neprazan zatvoren podskup kompletnog metričkog prostora čini kompletan metrički prostor. Obzirom da je
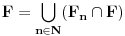
, i da su skupovi
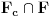
zatvoreni u

, postoji interval

i

takvi da je
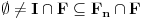
. Dakle,
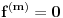
na
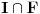
za sve
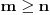
.
Neka je

maksimalan otvoreni podinterval od
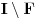
. Na njemu je funkcija

jednaka polinomu nekog stepena

. Ukoliko to nije nula polinom, važi da je
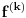
konstanta različita od nule na intervalu

. No, zbog neprekidnosti i jednakosti
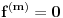
za sve
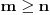
u bar jednoj od krajnjih tačaka intervala

(jer barem jedna pripada skupu

), važi
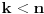
. Dakle, na svakom od takvih intervala je
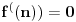
, pa pošto to važi i na skupu

, važi i na uniji, odnosno na celom intervalu

, odakle je funkcije

polinomijalna na

, što je u suprotnosti sa
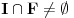
.
Dakle,
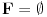
, pa je funkcija

polinomijalna.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
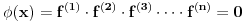
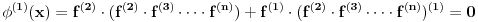
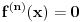 ,n-ti izvod polinoma n-tog stepena.
,n-ti izvod polinoma n-tog stepena.



 Re: Pokazati da je f polinom
Re: Pokazati da je f polinom