[es] - Racunanje limesa sa trigonometrijskim vrijednostima funkcija

neshto vishe
zgembo handislic

Član broj: 169878
Poruke: 132
*.teol.net.

Profil

Racunanje limesa sa trigonometrijskim vrijednostima funkcija

^{10.01.2013. u 09:20 - pre 149 meseci}

Na koji način se vrši računanje limesa sa trigonometrijskim vrijednostima funkcija?

Je li se tu koristi L'Hopital pravilo i primjenjuje određena smjena, u zavisnosti od zadatka?

Npr.

lim (((e^(5/x))-1) / (pi - 2arctgx)

x->+∞

lim (ln x) / (pi - 2x)^2

x->pi/2

Odgovor na temu

Fraktal
student
Beograd

Član broj: 305970
Poruke: 13
*.mbb.telenor.rs.

+1 Profil

Re: Racunanje limesa sa trigonometrijskim vrijednostima funkcija

^{10.01.2013. u 09:37 - pre 149 meseci}

Lopitala možeš primenjivati samo kod nekih limesa, ali to svakako ne zavisi od toga da li su ti limesi sa trigonometrijskim funkcijama ili ne (uzgred, ne znam zašto si dao drugi limes kao primer kada u njemu nema trigonometrijskih funkcija), već od toga da li limes neodređenog oblika tipa 0/0, beskonačno/beskonačno (ili se mogu svesti na neki od njih).

Dakle, princip rada sa limesima u kojem figurišu trigonometrijske funkcije je isti kao i kod drugih limesa. Na raspolaganju su ti razne transformacije, tablični limesi, Lopital (osim ako se ne traži rešenje bez korišćenja istog), razvijanje u red itd.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8703
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Racunanje limesa sa trigonometrijskim vrijednostima funkcija

^{10.01.2013. u 10:39 - pre 149 meseci}

Lopital se osim toga može primenjivati samo kada limes postoji, odnosno ne može se divergencija dokazivati njime. Ako po Lopitalovom pravilu izračunaš limes, onda on svakako postoji i to ne treba da dokazuješ, ali ako primenom Lopitalovog pravila dobiješ nešto divergentno, odatle ne možeš izvući nikakav zaključak, tj. onda je primena Lopitalovog pravila bila neuspešna.

Lopitalova teorema glasi da ako primenom Lopitalovog pravila (na oblik 0/0 ili beskonačno/beskonačno) dobiješ nešto konvergentno, onda ono od čega si pošao takođe konvergira i to ka istoj vrednosti. Precizije, ako su funkcije

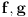
u nekom graničnom procesu

počev od nekle definisane, diferencijabilne i u tom graničnom procesu obe teže nuli ili obe određeno divergiraju ka beskonačnosti, onda je

.

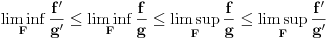
Prvi zadatak se lako rešava primenom Lopitalovog pravila, dok drugi nije nijednog od navedenih oblika, pa se Lopitalovo pravilo ne može primeniti. Drugi limes se računa neposredno.

Što se trigonometrijskih funkcija tiče, često se koristi činjenica da su sinus i kosinus ograničeni po apsolutnoj vrednosti jedinicom.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

neshto vishe
zgembo handislic

Član broj: 169878
Poruke: 132
*.teol.net.

Profil

Re: Racunanje limesa sa trigonometrijskim vrijednostima funkcija

^{10.01.2013. u 10:58 - pre 149 meseci}

Hvala vam ljudi. Ja bih u drugom zadatku primjenio smjenu: pi - 2x = t;
Onda bih dobio limes takav, gdje mi t->0;
Tako da bih u nazivniku imao t^2 (tu bi opet ostala vrijednost = 0), a u brojniku ln (pi / 2). Pošto je brojnik različit od nule, ne mogu primjeniti L'Hopital-a, ali onda vrijednost ovog mog limesa jeste beskonačna.

A prvi zadatak sam malo nesiguran. Brojnik je očigleddno = 0;
A nazivnik, hmm, pretpostavimo da je (pi - 2arctgx) = 0;
Onda imamo [0/0] i primjenu L'Hopital. Mene još zanima, da li u tom slučaju kod primjene L'Hopital važi, za neku funkciju f, kada x-> 0 v x->∞ za neke vrijednost f i g to, da lim f / g = lim f' / g' = lim f" / g" (jednako i njegovom drugom izvodu) ?

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8703
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Racunanje limesa sa trigonometrijskim vrijednostima funkcija

^{10.01.2013. u 11:45 - pre 149 meseci}

Svaku teoremu možeš primenjivati kad god su uslovi za njenu primenu ispunjeni. Ako dobijeni granični proces ispunjava uslove Lopitalove teoreme, možeš je primeniti. Međutim, to ovde nije slučaj, jer posle prve primene dobijaš oblik koji je neposredno izračunljiv.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

neshto vishe
zgembo handislic

Član broj: 169878
Poruke: 132
*.teol.net.

Profil

Re: Racunanje limesa sa trigonometrijskim vrijednostima funkcija

^{10.01.2013. u 12:14 - pre 149 meseci}

Svaka čast, hvala.
A sada, što se tiče one navedene formule (za Lopitalovo pravilo), pretpostavljajući da se ona može primjeniti i da su ispunjeni odgovarajući uslovi, interesuje me, kod nekih tipova zadataka, primjenom Lopitalovog pravila, tj prvog izvoda u brojniku i u nazivniku, ako se opet dobije neodređeni izraz, da li se može primjeniti drugi izvod u brojniku i u nazivniku, ili eventualno n-ti izvod u brojniku i u nazivniku?

Odgovor na temu

Fraktal
student
Beograd

Član broj: 305970
Poruke: 13
*.mbb.telenor.rs.

+1 Profil

Re: Racunanje limesa sa trigonometrijskim vrijednostima funkcija

^{10.01.2013. u 12:42 - pre 149 meseci}

Možeš Lopitalovo pravilo primenjivati u nizu neograničen broj puta, ako su zadovoljeni uslovi za njegovu primenu.
Dakle, ako prvom primenom Lopitalovog pravila dobiješ izraz koji je oblika 0/0 ili beskonačno/beskonačno onda opet možeš primeniti Lopitala.
Ukoliko ne, onda ne smeš. Sve to se može vrteti proizvoljan broj puta sve dok se dobija adekvatan neodređen oblik.

Odgovor na temu

neshto vishe
zgembo handislic

Član broj: 169878
Poruke: 132
*.teol.net.

Profil

Re: Racunanje limesa sa trigonometrijskim vrijednostima funkcija

^{10.01.2013. u 12:48 - pre 149 meseci}

Hvala još jednom.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8703
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Racunanje limesa sa trigonometrijskim vrijednostima funkcija

^{10.01.2013. u 13:14 - pre 149 meseci}

Trostruka primena Lopitalovog pravila se koristi na primer u računanju sledećeg limesa:

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

neshto vishe
zgembo handislic

Član broj: 169878
Poruke: 132
*.teol.net.

Profil

Re: Racunanje limesa sa trigonometrijskim vrijednostima funkcija

^{10.01.2013. u 13:29 - pre 149 meseci}

E super, zahvaljujem...

Odgovor na temu

different
student

Član broj: 190674
Poruke: 85
195.222.46.*

+4 Profil

Re: Racunanje limesa sa trigonometrijskim vrijednostima funkcija

^{11.01.2013. u 08:07 - pre 149 meseci}

Rjesenje prvog zadatka je 5/2.
Elementarnim rjesavanjem limesa bez upotrebe lopitalovog pravila zadatak se lako rjesava na sledeci nacin:
1. dodati u brojnik i nazivnik 5/x,
2. na osnovu toga limes (e^f(x)-1)/f(x) tezi jedinici ako f(x) tezi nuli kad x tezi beskonacno (a taj limes je tipski osnovni limes koji bi trebao znati rijesiti),
3.nakon toga dobija se novi limes lime x tezi besk. 5/x(pi-2arctgx),
4. sada se uvede smjena arctgx=u, x=tgu;x tezi besk.; u tezi pi/2, i dobija se novi limes lim u tezi pi/2 (5/tgu(pi-2*u));
5. nova smjena pi-2u=t, t tezi 0 i dobija se limes lim t tezi 0 (5/tg(pi/2-t/2)*t)=.....=5/2

www.portanaturae.com

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8703
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Racunanje limesa sa trigonometrijskim vrijednostima funkcija

^{11.01.2013. u 09:22 - pre 149 meseci}

Tako je. Ja sam stavio

, pa je ispalo 1/2. Sa

se dobija 5/2. Može se takođe koristiti činjenica da je

, što je za

jednako

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu