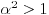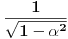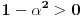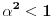Nikako ne uspevam da nateram
da mi prikaže \rightrightarrows - tako da (privremeno) odustajem

-koristiću \overrightarrow{\to}
I) Pošto zadatak ne bi imao smisla ukoliko dati integral ne konvergira - pozabavimo se prvo time.
Neka je
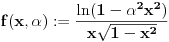
,
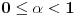
.
Vidimo da je:
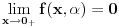
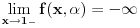
pa je singularitet samo u tački

. Takođe, smatraćemo da je
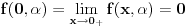
.
Neka je zato

i neka je
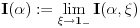
.
Pokazaćemo da je ovaj limes uvek konačan.
Dakle, dokažimo da
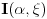
ravnomerno konvergira po
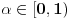
kad
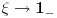
tj. da
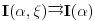
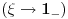
.
Upotrebićemo
Vajerštrasov kriterijum i pri tom, budući da na konvergenciju utiče samo ponašanje podintegralne f-je u nekoj okolini singulariteta - posmatraćemo f-ju na intervalu
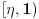
za neko fiksirano

.
Za svako
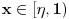
i svako
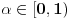
važi:
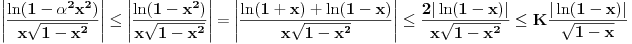
za neko
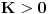
.
To je posledica neprekidnosti (pa samim tim i ograničenosti) f-je
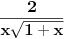
na kompaktnom skupu

(pa time i na
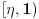
) a upotrebljeno je i

što je posledica važenja relacije
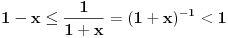
na
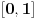
.
Parcijalnom integracijom dobijamo
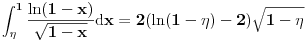
čime je dokazano
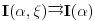
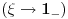
.
U narednim tačkama koristiću neke osnovne teoreme - da ih ne bi prekucavao, pozivaću se na njihovu numereciju u drugom izdanju knjige
Matematička analiza 2,
D. Adnađević, Z. Kadelburg.
1. Treba ispitati neprekidnost f-je
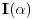
. Možemo da upotrebimo neprekidnost f-je

na
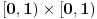
pa rezultat direktno sledi na osnovu teoreme
7.3.2.
A možemo i da se malo pomučimo (ipak je to zadatak sa ispita

) i upotrebimo teoremu
7.3.1 jer imamo da int. ravnomerno konvergira a i za svako
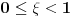

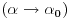
na
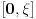
za svako
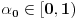
. Evo odakle to sledi:
Neka je

dato.
F-ja
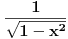
je neprekidna (pa i ograničena nekim
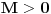
) na
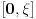
.
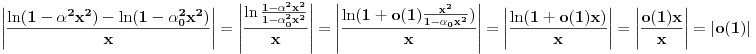
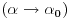
- ovo poslednje sledi iz ograničenosti neprekidne f-je
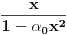
na
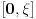
.
Sada je jasno da postoji
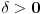
tako da iz
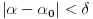
sledi
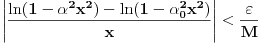
, pa najzad imamo

za svako
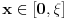
što tačno znači da

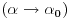
pa iz teoreme
7.3.1 sledi
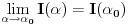
.
2. Ovde bi mogli da upotrebimo teoremu
7.3.3 (dovoljni uslovi za upotrebu
Lajbnicovog pravila na nesvojstvene parametarske integrale), ako pokažemo da važe svi potrebni uslovi.
i) f-ja
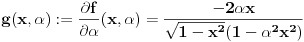
je neprekidna na
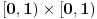
.
ii) Za svako
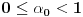
integral
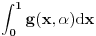
ravnomerno konvergira na
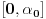
. To sledi na osnovu
Vajerštrasovog kriterijuma:
za svako
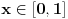
i svako
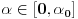
važi
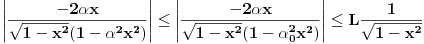
za neko
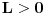
- to sledi iz ograničenosti f-je
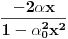
na
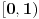
(gledano kao f-ja po

). Ravnomerna konv. sledi zbog konvergencije integrala

.
iii) 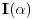
(ravnomerno) konvergira na
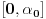
time su provereni svi uslovi pa na osnovu teoreme
7.3.3 sledi tvrđenje pod
2.
3. Sada moramo da izračunamo
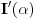
- jer bi nam to moglo pomoći u pronalaženju
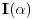
.
U integralu
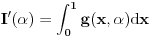
uvodimo smenu
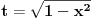
.
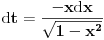
integral postaje

Dakle, imamo da je
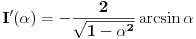
a odatle odmah dobijamo
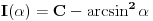
.
Na osnovu definicije f-je
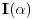
vidimo da je

.
Budući da sam ovo ukucavao/proveravao direktno u polju za upis odgovora - valjda ne moram da objašnjavam koliko sam se napatio
 [Ovu poruku je menjao uranium dana 24.08.2006. u 02:17 GMT+1]
[Ovu poruku je menjao uranium dana 24.08.2006. u 02:17 GMT+1]
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.
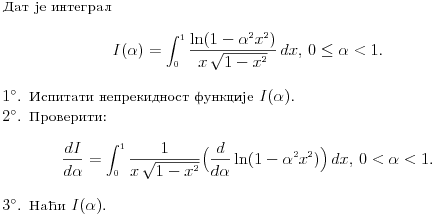
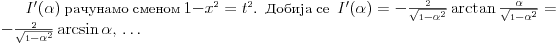
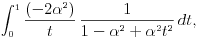
 ne može da se primeni??! Ako može, zašto taj
ne može da se primeni??! Ako može, zašto taj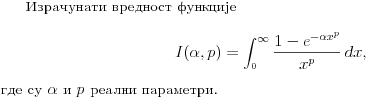
 i
i 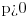 podintegralna
podintegralna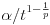 za
za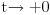 , a
, a 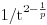 za
za . Ja dobijam da je:
. Ja dobijam da je: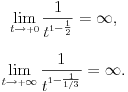




 Parametarski integrali, singulariteti, ... nocna mora!
Parametarski integrali, singulariteti, ... nocna mora!
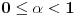
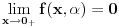
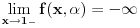

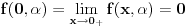

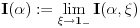
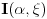
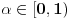
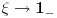
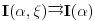
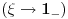
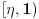

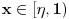
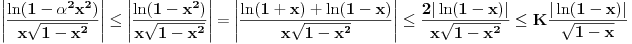
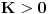
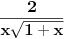


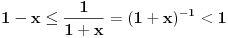
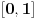
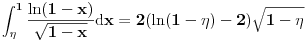
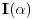

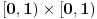
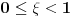

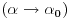
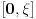
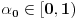

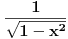
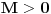
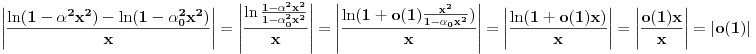
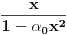
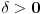
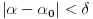
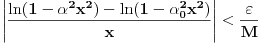

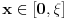
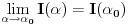
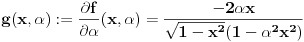
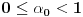
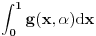
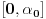
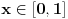
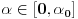
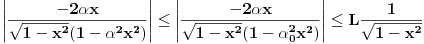
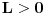
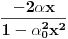
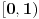


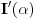
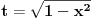
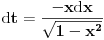

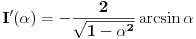
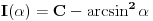

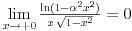
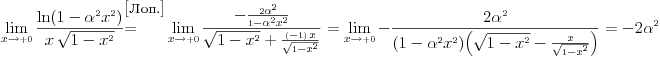
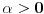
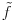
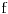
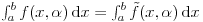
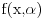

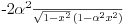
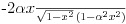
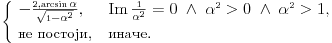
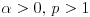
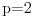
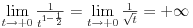
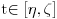
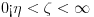
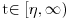
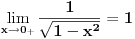
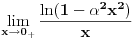
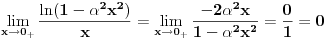
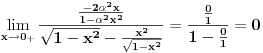
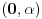


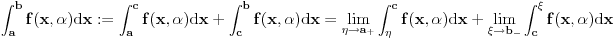
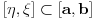

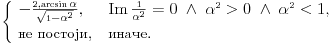
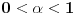
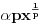
 Re: Parametarski integrali, singulariteti, ... nocna mora!
Re: Parametarski integrali, singulariteti, ... nocna mora!