Pa ovako:
Znaci, imamo niz i treba da vrsimo operacije add (int x, int val) koje dodaju x-tom elementu vrednost val, i sum (int x) koja vraca sumu prvih x clanova niza. Dakle, najprostiji algoritmi koji bi nam pali na pamet za ovaj problem su npr da u jednom nizu pamtimo vrednosti samog niza, koje se unose, i da ih stoga add bude slozenosti O (1), a da sabiramo obicnom for petljom, sto bi bilo O (n), za sum f-ju. Ili mozemo u a [ i ] da pamtimo zbir od a [1] do a [ i ], pa da sum bude u O (1), ali bi add bilo u O (n), jer bi morali da povecavamo sve od a [ i ] do a [n]. E, slozenost O (log n) za obe f-je se postize primenom kumulativnih tabela, i to je "as good as it gets". Dakle, imamo niz tree, od n elemenata. (primetimo da je indexiranje od 1 do n, a ne od 0 do n - 1). E sad, svaki broj znamo da moze da se predstavi kao zbir stepena dvojke. Pa onda i svaka ovakva suma moze da se predstavi kao zbir odredjenih "podsuma". Kakvih ? Pa, ovako, ako treba da recimo nadjemo sum (i), mi cemo to radimo na sledeci nacin: sabiramo tree [ i ] sve dok i nije nula, a posle svakog sabiranja broju i "izbrisemo" najdesniju jedinicu u binarnom zapisu (pretvorimo je u 0). To ce reci da je recimo sum (13) = tree [13] + tree [12] + tree [8]. Slozenost ovog koraka bi bila O (log n), jer broj ima O (log n) cifara u binarnom zapisu. E sad ostaje jos kako da pamtimo vrednosti tako da u tree [13] bude a [13], u tree [12] bude a [9..12] i u tree [8] bude bas a [1..8]. U sustini, u tree [ i ] treba da bude a [k + 1..i] gde je k prvi broj manji od i koji je deljiv sa vecim stepenom dvojke nego i. To ce reci da je npr za sve neparne brojeve i tree [ i ] = a [ i ]. Npr tree [6] = a [5] + a [6], jer je 4 prvi manji od 6 da je deljiv sa vise od
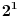
. Dakle, kad treba da updete-ujemo tree, tj da odradimo add, radicemo obrnuto nego za sum. Za add (x, val) dodacemo val u tree [x], pa u tree [k], gde je k prvi sledeci broj veci od x koji je deljiv sa vecim stepenom dvojke nego x, pa u tree [r], r prvi veci od k, da je "vise" deljiv sa dvojkom nego k, itd. Treba se malo potruditi da se sve ovo razume, a kad se ukapira, ono sto je vise nego lepo je kod koji je izuzetno jednostavan (treba obratiti paznju na operacije nad bitovima koje raditi gore opisane radnje):
Code:
int sum (int x)
{
int tempsum;
if (x == 0)
return 0;
tempsum = 0;
while (x > 0)
{
tempsum += tree [x];
x &= x - 1;
}
return tempsum;
}
Code:
void add (int x, int val)
{
int temp;
do
{
tree [x] += val;
if (x == 0)
break;
temp = x; // Ovo je u sustini isto sto i
temp &= -x; // x = x + x & (-x), ali ja
x += temp; // vise volim da pisem ovako
}
while (x <= n);
}
I HAD A NIGHTMARE
IT ALL STARTED NORMAL
10101010
10110011
THEN ALL OF A SUDDEN
1100102
GAAAAH
_____________________________
www.princeton.edu/~skrstic
www.niwifi.co.sr
Kumulativne tabele
Registrovani: 3 ( Nebojsa Milanovic, vjova, Edithabsen )
Re: Kumulativne tabele