Jednostavan način da se utvrdi da li se dve duži seku je da se ispita
položaj krajnjih tačaka jedne duži u odnosu na drugu duž. Preseka ne
može biti ako obe krajnje tačke leže sa iste strane duži. Ovu proveru
svako zna da izvede, samo je pitanje kako izabrati računski
najjednostavniji način.
Probaću da predložim jednu mogućnost.
Da bih nastavio sa objašnjavanjem, moraću da uvedem sledeću
notaciju. Neka su date duži

i

svojim
krajnjim tačkama. Za prvu duž to su tačke
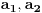
, a za
drugu
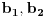
. Sve tačke date su svojim koordinatama, na
primer
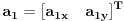
.
Uvedimo vektor duži
sa:
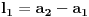
i slično
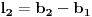
. Par
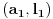
takođe potpuno određuje duž. Neka je duž

,,prva``, a

,,druga``.
Želimo da proverimo da li se tačke druge duži nalaze sa iste strane
prve duži. To ćemo uraditi tako što nađemo projekciju vektora

i
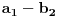
na normalu na prvu duž i proverimo
da li projekcije imaju isti znak. Ako imaju, onda preseka ne može biti
(dokaz sledi).
Normalu možemo pronaći rotacijom duži
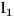
za
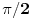
transformacijom
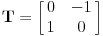
, i nalaženjem proizvoda
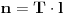
. Ovo se lako
računa jer je potrebna samo operacija promene znaka.
Dakle, neka su date vrednosti projekcije prve i druge razlike
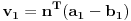
i
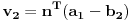
i neka su obe tačke druge duži sa iste strane
prve duži, dakle
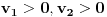
.
Sve tačke na drugoj duži su date sa:
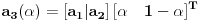
Za projekciju svake tačke na drugoj duži važi:
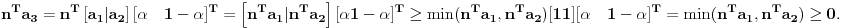
Dakle svaka tačka na drugoj duži ima projekciju istog znaka kao
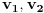
pa nema preseka, tako da možemo vratiti vrednost
false kao odgovor na pitanje da li presek postoji.
Ako makar jedna od dve provere pokaže da su tačke na drugoj duži sa
iste strane prve duži, preseka nema. Ukoliko oba preseka postoje,
postoje vrednosti

u obe provere koje ispunjavaju
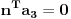
, tj. preseci se nalaze između krajnjih tačaka
odgovarajućih duži. Kako je presek jedinstven, oba rešenja se odnose
na istu tačku. Možemo vratiti vrednost
true kao odgovor
na pitanje da li se duži seku.
Kao što vidite, pri računanju koristimo samo računanje skalarnog
proizvoda, poređenja i promenu znaka tako da bi postupak trebalo da
bude (računski) jednostavan. Izbegava se deljenje pa prema tome i singulariteti.
f
[
Ovu poruku je menjao filmil dana 02.06.2003. u 00:51 GMT]
[
Ovu poruku je menjao Gojko Vujovic dana 04.02.2004. u 18:01 GMT]